Sequential learning involves learning to organize sequences of behavior or to anticipate events that occur in a consistent sequential order. Despite a century of research directed toward characterizing how acquired sequential behavior is organized, many questions remain unanswered regarding the nature of the mechanisms responsible for sequential in animal behavior. Perhaps the question that has proven most difficult to answer has been whether or not relational structures that are present in a sequence to be learned influence how and what animals learn. That is to say, when presented with structured sequences, do nonhuman animals encode a memorial representation of their experience that “the information given” (Bruner, 1957)? Do they ultimately abstract and learn relational information—do they induce and learn rules? In this paper, I hope to provide an overview of the current evidence that bears on this question from our recent behavioral and psychobiological research on rat sequential learning. First, I will describe some behavioral studies from the 1970s and 1980s that seemed to show that rats indeed learn rules from patterns composed of sequences of food quantities, and then I will describe our recent research with a computational model that questioned the necessity of that conclusion. Next I will describe more recent operant research from our laboratory consistent with the idea that rats are sensitive to the structure of patterns that are hierarchically organized or composed of two interleaved subpatterns. Finally, I will present data from drug and lesion studies that suggest that sequential learning in rats is mediated by multiple concurrent psychological and brain systems, at least one of which appears to be related to rule induction.
Rule Induction in Reward Magnitude Serial Pattern Learning
In the 1970s and 1980s, several studies by Stewart Hulse and colleagues were taken as strong evidence that rats can abstract formal structure from the patterned sequences of events (“serial patterns”) they learn to anticipate. Hulse and Dorsky (1977; 1979) created serial patterns from a stimulus “alphabet” (Jones, 1974) of various quantities of food (cf. Hulse, 1973) presented to rats in a series of trials in runways. The patterns they created varied in formal structure. A strongly monotonic sequence of 14-7-3-1-0 food pellets was formally simple in structure, requiring a single “less than” rule to describe the relationships of all successive pairs of quantities. A weakly monotonic 14-5-5-1-0 pattern and a nonmonotonic 14-1-3-7-0 pattern were progressively more complex, requiring combinations of “less than,” “greater than,” and “equal” rules to adequately describe the patterns. Rats learned to track the formally simple monotonic pattern most rapidly and to the most proficient level of tracking performance of the three patterns, followed by the weakly monotonic and the nonmonotonic patterns. Hulse and Dorsky ruled out a variety of pattern-learning strategies the rats might have adopted to learn these patterns in favor of the hypothesis that rats are sensitive to pattern structure and learned the rules that described the structure (see Hulse and Dorsky, 1977). The implication was that rats did not have to rely on chaining or remote associations alone to master sequences.
Two additional studies were used as evidence that the rules rats learned from serial-patterns were, in fact, abstract. In one study (Hulse & Dorsky, 1979), rats demonstrated the ability to generalize a rule from one set of patterns to a different pattern. In a second study, Fountain and Hulse (1981) evaluated rats’ ability to extrapolate patterns of varied structural complexity. Rats were better able to predict a new 0-pellet element added to a structurally simpler 14-7-3-1 pattern than 0 pellets added to a structurally complex 14-3-7-1 pattern. The authors reasoned that the monotonic pattern produced better anticipation of “0” than the nonmonotonic pattern because the monotonically decreasing 14-7-3-1 sequence was described by a single “less than” rule that would lead naturally to anticipation of “0” after “1”.
Capaldi and colleagues (e.g., Capaldi & Molina, 1979) and Haggbloom and colleagues (e.g., Haggbloom, 1985) challenged the theory that rats learned rules by reporting evidence that stimulus associations and generalization played important roles in pattern learning. Simply put, this view supposed that food quantities earlier in a sequence serve as cues for the later food quantities. According to this view, acquisition depends in part on discriminability and salience of pattern elements, but learning and performance are also determined by generalization between food quantity signals. Evidence supporting this interitem association or “item memory” view came from various runway studies. First, Capaldi and Molina (1979) demonstrated that a structurally complex sequence constructed from highly discriminable elements (1-29-0) produced better pattern tracking relative to a structurally simple sequence constructed of less discriminable elements (20-10-0). Second, in response to Hulse and Dorsky’s (1977) rule generalization studies, Haggbloom (1985) demonstrated that pattern tracking was disrupted upon transfer only when associative information was removed, but was unaffected by manipulations that violated rule or serial position information. Finally, Haggbloom and Brooks (1985) showed that discriminability of pattern elements, not pattern structure, was the best predictor of pattern extrapolation. In subsequent studies, both camps provided additional evidence that rat sequential behavior could be described in terms of rule learning theory or item memory theory, but the debate was never adequately resolved.
One of the problems in the serial-pattern learning literature that complicated the rule learning versus item memory debate was that item memory theory with generalization could not make strong predictions concerning patterns that contained more than a few elements. For example, Capaldi, Verry, and Davidson (1980) stated that the “generalized reward- signal capacity” received by “1” in sequences such as 14-7-3-1-0 or 14-5-5-1-0 was “completely indeterminate” (p. 583). In other words, even though “1” signaled nonreward (“0”) by way of direct association, item memory theory predicts that cue generalization should cause “1” to acquire the ability to signal reward through generalization from other similar items in series. It was thought that the amount of generalization was crucial in that it determined how much “1” would signal reward versus nonreward. However, the amount of reward-signal capacity “1” received through generalization was indeterminate presumably because Capaldi et al. could not explicitly describe the requisite generalization functions for food reward quantities. For that reason, Capaldi et al. (1980) were unable to make strong predictions regarding learning for 5-element series that would have allowed them to claim that item memory theory could describe the available behavioral data. Instead, at the time they were forced to adopt the weaker position that the item memory interpretation “cannot be excluded” (Capaldi, Verry, & Davidson, 1980).
One approach to determining whether complex behavior can be described by a few simple assumptions is to use a mathematical model to simulate the behavior. To help us determine whether pairwise association and generalization of cues might account for rat reward magnitude serial pattern learning, we recently sought to use a computational model to conduct simulation studies. In considering how to begin to model serial pattern learning processes, a variety of different computational approaches were considered from simple stochastic models, to connectionist models, to production system approaches. Each of these varieties of computational models has been applied to sequential learning and memory problems at one time or another. For example, “random walk” models have been advanced by Roitblat and, recently, Neath and Capaldi (1996), connectionist models have been advanced by Roitblat (Roitblat, 2002), and a forerunner of production system models was pioneered on serial-pattern learning problems studied in humans by Simon, Newell, and their associates (Newell & Simon, 1961; Simon & Kotovsky, 1963). The principal concern was that the model should associate specific items in “memory” and produce generalization phenomena. A connectionist analog was chosen because it has these properties, and stochastic models and production systems were rejected because they are not easily stated in terms consistent with basic principles of discrimination learning. Several varieties of connectionist and related models have the desired properties and, thus, also bear at least superficial resemblance to Capaldi’s item association and cue generalization ideas. In particular, the TODAM model developed by Bennett Murdock (Murdock, 1982; 1983) and the CHARM model developed by Janet Metcalfe (Metcalfe Eich, 1982; Metcalfe, 1990) have these properties. These models have the added advantage that both Murdock’s and Metcalfe’s models have also been used successfully to simulate a broad array of human associative learning and memory phenomena (Metcalfe, 1990; 1993; Murdock, 1983; 1992), including some rote sequential learning phenomena (Murdock, 1983; 1992; 1995).
We conducted simulation studies with a computational model of sequential learning we called the Sequential Pairwise Associative Memory (SPAM) model (Wallace & Fountain, 2002; 2003). SPAM includes all of the essentials of the TODAM model described by Murdock (1982; Murdock, 1983) and Metcalfe (Metcalfe Eich, 1982; Metcalfe, 1990) and subsequently used by Metcalfe (1990) as the model known as CHARM in her simulations of eyewitness misinformation effects and “blending” of memories that depend on stimulus association and generalization. The model is described in great detail by Murdock (1982; 1983; 1985) and Metcalfe (Metcalfe Eich, 1982; 1990) and also in our studies (Wallace & Fountain, 2002; 2003). SPAM is also one possible instantiation of the item memory view because encoding is based on pairwise associations of items in memory and because generalization occurs between similar cue items.
When successive pairs of items are associated in SPAM, the result of the association process is added to a common trace. Because the trace is a composite of all prior associations, retrieval can result in generalization when the same or similar cue items were earlier associated with two or more different items. This is the basis of generalization in SPAM. For example, items are represented by vectors in SPAM. Items such as “14 pellets”, “7 pellets”, “3 pellets”, “1 pellet”, and “0 pellets” are represented by vectors. Since these items represent quantities of food that presumably vary systematically in similarity to each other, we used vectors that varied systematically in similarity to represent them (as Metcalfe (1990) did in her studies of “blended memories” in eyewitness testimony). Under these conditions, if the composite trace contains information about the association of “1” and “0” only, cueing the composite trace with “1” retrieves “0.” On the other hand, if the composite trace contains the associations “3” with “7” and “1” with “0”, cueing the trace with “1” retrieves both “0” (retrieved directly by “1”) and, to a lesser degree, “7” (cued by generalization of “1” to “3,” since “1” and “3” are similar). This generalization would result in an “anticipation” of a quantity greater than “0.” This effect is reminiscent of generalization typically observed in discrimination learning and it is also reminiscent of Capaldi’s idea of cue generalization, where the capacity to signal reward or nonreward can generalize from one cue to other similar cues. Because SPAM is an associative model that has characteristics of simple associative systems, namely, pairwise associations and generalization, it was used to test whether an instance of this type of mechanism could account for the phenomena that various investigators have reported in their studies of rat reward magnitude pattern learning.
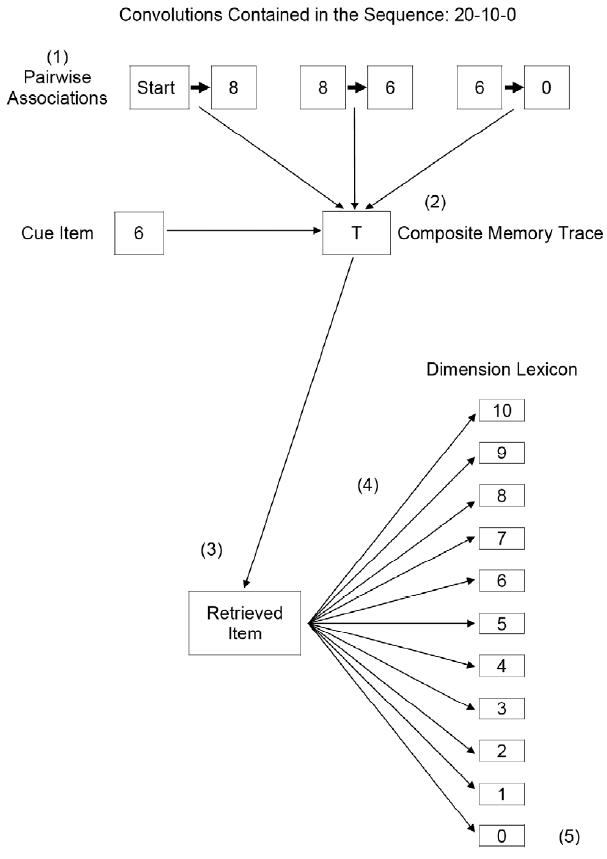
Figure 1. Flow diagram for one iteration of the SPAM model for the sequence 20-10-0 (coded as vector 8-vector 6-vector 0) with “6” as a cue for the anticipated item. The schematic depicts the following steps: (1) association by convolution, (2) storage in a composite memory trace, (3) retrieval by correlation of a cue item with the composite memory trace, (4) determining dot products (similarity) of the retrieved item vector and each individual lexicon item vector, and (5) recognition by selecting the lexicon item with the highest similarity to the retrieved item. Note. From “What is learned in sequential learning? An associative model of reward magnitude serial-pattern learning,” by D. G. Wallace and S. B. Fountain, 2002, Journal of Experimental Psychology: Animal Behavior Processes, 28, 43-63. Copyright 2002 by the American Psychological Association. Reprinted with permission.
Figure 1 provides a schematic of the general steps involved in an iteration of the computational model. Each iteration represents 1) a rat’s encoding of the sequence and 2) its response to the final element of the sequence having been cued by the next-to-last element. For example, a simulation of performance for a 20-10-0 sequence would include three associations, hereafter called “convolutions.” The first convolution would be Start-8, where “Start” is an independent item vector representing distinctive cues signaling the first trial of the sequence and Item Vector 8 represents 20 pellets of food. Later convolutions would be 8-6 and 6-0. The convolution process is labeled “(1)” in Figure 1. The item that was convolved with 0, namely, 6, was later used to cue the composite memory trace, labeled “(2)” in Figure 1, to recover a retrieved item, labeled “(3)”, through the process of “correlation.” The retrieved item was then compared to each item in the lexicon. The lexicon was “dimensional”, that is, the lexicon contained all the items of the stimulus dimension representing food quantity. The comparison process generated dot product values that reflected the degree of similarity between the retrieved item and each individual item in the lexicon, as indicated by “(4)” in Figure 1. The lexical item with the highest dot product value was chosen as the item best predicted by the cue for that iteration, shown as “(5)” in Figure 1. In order to obtain a good representation of the central tendency of the program’s performance, 1000 iterations were performed for each sequence simulation. Proportion responding to an item in the lexicon was used to calculate anticipated item scores that are considered analogous to running speeds elicited by the cue associated with the final item of the sequence. A smaller anticipated item represents slower running, and runway latency should be directly proportional to this score. For a detailed mathematical description of convolution, correlation, and the calculation of anticipated item scores, see Wallace and Fountain (2002; 2003).
In a series of simulation studies (Wallace & Fountain, 2002), we used SPAM to test whether simple associative processes, namely, pairwise association and generalization, could account for some of the fundamental behavioral evidence described by Hulse, Capaldi, and colleagues. In two simulation studies (Wallace & Fountain, 2002), SPAM predicted that a short pattern with highly discriminable elements would be learned better than one with less discriminable elements even though the former was monotonic, that is, formally simple, and the latter was nonmonotonic, that is, formally more complex (Capaldi & Molina, 1979). This prediction from the model might be expected given the similarities of SPAM and item memory theory, but SPAM also predicted that a long, strongly monotonic pattern of food quantities should be tracked better than a long nonmonotonic pattern, as observed by Hulse and Dorsky (1977). In two other simulation studies (Wallace & Fountain, 2002), SPAM also successfully simulated behavioral “rule generalization,” “extrapolation,” and associative transfer data (cf. Fountain & Hulse, 1981; Haggbloom, 1985; Haggbloom & Brooks, 1985; Hulse & Dorsky, 1979).
The critical point of this discussion is that over a broad range of parameter values (Wallace & Fountain, 2002; 2003) SPAM simulations demonstrated the power of simple associative principles of pairwise association and stimulus generalization, account for rats’ performance in patterns of different length and item arrangements (Wallace & Fountain, 2002; 2003), “rule generalization”(Wallace & Fountain, 2002), and pattern “extrapolation” (Wallace & Fountain, 2002). SPAM is nearly the simplest possible formulation of this associative memory model because it does not store information about remote associations between sequential events, the effects of extraneous cues like phrasing, or about the passage of time or serial position. This is not to say that these factors play no role in serial-pattern learning; our SPAM simulations simply tested whether a model without these features could be sufficient to describe what may be considered the critical phenomena for the rule learning versus item memory debate in the reward magnitude serial pattern learning literature (Wallace & Fountain, 2002). It should be noted that we also concluded that SPAM is likely not unique; it is likely a member of a class of formally equivalent or similar associative models that share common features—association and generalization— that should produce common behavioral outcomes in sequential learning paradigms (Wallace & Fountain, 2002). Prior unpublished work in our lab restating SPAM with an error-correcting rather than a Hebbian learning rule supports this contention (Wallace, Lewis, Fountain, & Block, 1999). The important conclusion is that there exists at least one subsymbolic mechanism—SPAM—that can explain sequential behavior of a type previously thought to require rule induction processes (Gallistel, 1995; Hulse, 1978; Lashley, 1951; Roitblat & von Fersen, 1992).
Although rats may in fact use rule induction processes to learn serial patterns, SPAM simulations indicate that this is not a necessary conclusion from the classical behavioral studies on reward magnitude sequential learning. SPAM’s success also argues that computational models can play a role in animal cognition research. In this case, SPAM demonstrated that complex behavior can sometimes result from the aggregate effects of simple behavioral processes acting in complex settings, and that computational modeling may be required to demonstrate that simpler processes are viable alternatives to more complex processes as explanations. Computational modeling provides one means of maintaining our vigilance regarding the ever-present dangers of the argument from design (Blumberg & Wasserman, 1995) in animal cognition theorizing (cf. Church, 1997; 2001). Argument from design in this context would suggest that putative rule learning phenomena such as sensitivity to pattern structure, rule generalization, and pattern extrapolation are too complex to be described by simpler processes. Instead, so the argument from design goes, these behavioral phenomena by their very complexity imply a higher-order symbolic process, presumably a rule learning process capable of inducing and encoding a memorial representation of abstract relational rules that describe pattern structure. SPAM provides an existence proof for a purely associative item memory mechanism that can account for these reward magnitude pattern learning phenomena without resort to such processes. Stronger evidence for rule learning in rats is necessary to substantiate such strong claims. In the following discussion, I will describe evidence for rule induction in rats from another paradigm we developed to overcome some methodological limitations of the reward magnitude serial pattern learning paradigm.
Hierarchical Structure, Phrasing Effects, and Rule Induction in Response Sequence Learning
We have conducted a number of studies to examine the extent to which pattern structure influences how rats learn to produce long and elaborate patterns of responses. In behavioral studies, drug injection studies, and brain lesion studies in our lab, rats learn to perform complex serial patterns that involve pressing levers in a circular array in the proper sequential order. Rats are trained in an octagonal operant chamber equipped with a retractable lever mounted on each wall designated 1-8 in a clockwise fashion (see Figure 2). In the typical procedure, all levers are presented at the beginning of each trial and the rat can press any of the 8 levers. If the correct lever is chosen, the rat receives brain-stimulation reward (BSR) via implanted hypothalamic electrodes. If an incorrect lever is chosen, all levers except the correct lever withdrawn from the box and the rat must make a correct choice to receive BSR before continuing to the next trial. The latter procedure has been used with much success to analyze sequential behavior in extremely long serial patterns (up to 60 elements in length) and in probe pattern procedures that involve up to 175 complete patterns each daily session. For more details on the method, see Fountain, Rowan, et al. (2006).

Figure 2. Layout of retractable levers in a circular array in an octagonal operant chamber. Digits indicate the position of levers in the array. Rats were reinforced with pulses of brain-stimulation reward (BSR) for choosing the levers in the correct sequential order on successive trials.
Two common patterns we have required rats to learn in this paradigm are a structurally “perfect” pattern versus a pattern virtually identical to the first but containing a single element at the end of the pattern that violates the otherwise simple structure:
Perfect pattern: 123-234-345-456-567-678-781-812- (…repeat pattern)
Violation pattern: 123-234-345-456-567-678-781-81- (…repeat pattern)
where digits indicate the clockwise position of the correct response on successive trials and dashes indicate brief pauses that serve as “phrasing cues.” It should be noted that these 24-element response patterns can be characterized as composed of eight 3-element “chunks” that share a common base “rule” within chunks, namely, “+1” or “move-one-clockwise.” This rule is consistent except after phrasing cues at “chunk boundaries”—where rats encounter transitions between phrases (chunks) of the pattern—and on the last element of the violation pattern (the underlined element “8”). The first element of each new chunk is thus termed a “chunk boundary element” that is a transition between phrases (chunks) of the pattern. The last element of the violation pattern is an “exception-to-the-rule” because applying the expected within-chunk “+1” rule at that point should produce a response at position “2” in the array, not the required “8” response. We call this a “violation element” because it blatantly violates the base within-chunk rule that consistently predicts a correct response in the third position of every other chunk of the pattern. Perhaps not surprisingly, evidence from our lab indicates that rats learn associations so that phrasing cues become discriminative stimuli that cue responses after the phrasing cue (Fountain, Benson, & Wallace, 2000; Stempowski, Carman, & Fountain, 1999; Wallace, Rowan, & Fountain, in press) and rats also learn to use combinations of multiple pattern elements leading up to a violation element to anticipate it and respond properly on the violation trial (Fountain, 2006). In what follows, I will focus on evidence that rats also abstract pattern structure from response sequences they learn to perform.

Figure 3. The structures of the 3-level hierarchical and the linear patterns rats learned in the octagonal operant chamber. The Hierarchical pattern is described by a formally simple completely nested rule structure: elements within 3-element chunks are related by first-order rules, chunks within the first and second halves of the pattern, respectively, are related to each other by second-order rules, and the first half of the pattern is related to the second half of the pattern by a third-order “mirror” rule. The incompletely nested Linear pattern was generated by exchanging two 3-element chunks of the Hierarchical pattern (underlined and in red). In this structure, elements within any chunk are related by a rule, but chunks are not related to each other systematically.
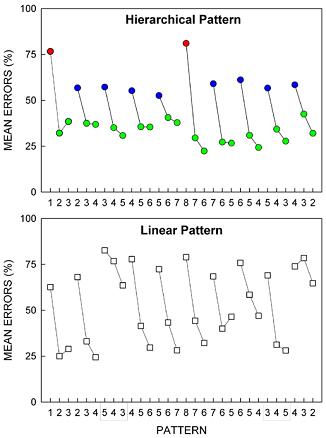
We tested whether pattern structure would determine the ease or difficulty of pattern learning by developing patterns with hierarchical structure, then reordering chunks of the pattern to produce “linear” structure, that is, a sequence of unrelated chunks, as shown in Figure 3. The results showed that pattern complexity predicted pattern learning difficulty (Fountain & Rowan, 1995a). The Hierarchical pattern was easier to learn than the less structured Linear pattern. In addition, for rats in the Hierarchical group, the difficulty of learning to respond appropriately on any trial was a function of the hierarchical level of the rule required to predict the item. As shown in Figure 4, Hierarchical rats produced significantly more errors on the first trial of Chunks 1 and 6 (red circles in Figure 4) than on all other trials. These trials corresponded to the highest-order rule transitions in the pattern structure (i.e., third-order rule transitions). Fewer errors were observed on the first trial of other chunks (blue circles), trials corresponding to second-order rule transitions. The fewest errors occurred within chunks (green circles) where trials corresponded to first-order rule transitions. Thus, in the completely hierarchical pattern, the difficulty of learning to respond appropriately on any trial was a function of the hierarchical level of the rule required to predict the item. Linear rats did not show the 3-level hierarchical pattern of errors observed for Hierarchical rats. Linear rats responded as though elements within most chunks were predictable, but that chunks were somewhat haphazardly arranged (Fountain & Rowan, 1995a).
Figure 4. Rats’ mean percentage of pattern tracking errors for hierarchical and linear patterns (top and bottom panels, respectively) as a function of the 30 items of the patterns. Mean percentage of errors are shown for the first week of training. Note that in the hierarchical pattern data, errors were most frequent at the highest-level 3rd-order rule transitions at the beginning of each half of the pattern (red circles), next most frequent at the 2nd-order rule transitions at the beginning of other chunks (blue circles), and least frequent at 1st-order rule transitions within chunks (green circles), as predicted by rule learning theory. Note. From “Coding of hierarchical versus linear pattern structure in rats and humans,” by S. B. Fountain and J. D. Rowan, 1995, Journal of Experimental Psychology: Animal Behavior Processes, 21, p. 187-202. Copyright 1995 by American Psychological Association. Adapted with permission. Rats found learning a completely nested hierarchical pattern easier than learning a less organized pattern even when pairwise associations and pattern length were conserved across patterns. In another study from the same series (Fountain & Rowan, 1995a), a 3-level hierarchy was easier to learn than a 4-level hierarchy when pattern length was conserved across patterns. As a rule, then, pattern complexity was a |
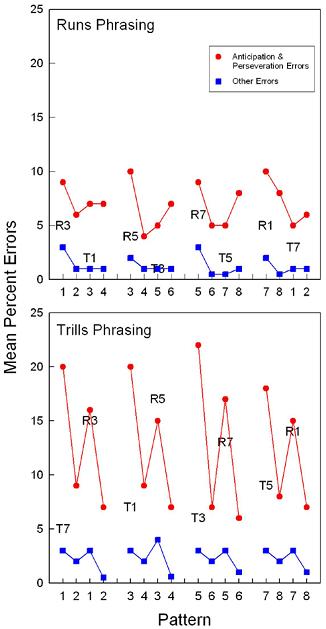
Figure 5. Rats’ group mean element-by-element percent error rates collapsed across both weeks of the experiment for Runs and Trills groups (top and bottom panels, respectively). Both graphs show error rates for overextension errors consistent with a runs (R) or trills (T) interpretation of the structurally ambiguous pattern, rates of responses identified as anticipation and perseveration errors, and the rates of other errors that could not be classified into these categories. Note. From “Encoding structural ambiguity in rat serial pattern learning: The role of phrasing,” by S. B. Fountain, J. D. Rowan, and H. M. Carman, 2007, International Journal of Comparative Psychology, 20, 25-34. Copyright 2007 by International Society for Comparative Psychology. Adapted with permission. |
better predictor of acquisition difficulty in these studies than was pattern length. These acquisition results are evidence that pattern structure can be an important determinant of pattern difficulty for rats learning response sequences. In another octagonal chamber study, we examined the effects of phrasing a structurally ambiguous pattern as either a series of “runs” or “trills” (Fountain, Rowan, & Carman, 2007). A 1234345656787812 pattern phrased as runs (1234- 3456-5678-7812…) was easier to learn than when it was phrased as trills (1212-3434-5656-7878), a result that resembles a similar “run bias” reported in the human sequential learning literature and in earlier studies of rats’ response to “run” versus “trill” structures (Fountain & Rowan, 1995b). Whereas rats learning the runs-phrased pattern showed rapid learning and little tendency to make trills errors, rats learning the trills-phrased version of the pattern produced inflated rates of both trills and runs errors, as shown in Figure 5 (Fountain et al., 2007). The results show that rats represented the runs- and trills-phrased versions of the pattern differently. These results add to the evidence that, in addition to serving as discriminative cues, phrasing cues can bias pattern perception in rat serial pattern learning resulting in memorial representations characterized by multiple interpretations of the same pattern.
Rule Induction in Interleaved Pattern Learning
Humans have the ability to chunk together information from nonadjacent serial positions in sequential patterns. For example, human subjects can extrapolate the pattern, AMBNCODPE_, to find the missing element, “Q,” by sorting pattern elements into two component interleaved subpatterns: ABCDE and MNOP_. We have conducted several experiments to investigate rats’ ability to reorganize pattern elements from nonadjacent serial positions into chunks not presented by the experimenter (Fountain & Annau, 1984; Fountain & Benson, Jr., 2006; Fountain, Rowan, & Benson, Jr., 1999). Generally, the question of interest is whether rats learn interleaved subpatterns at different rates as a function of subpattern complexity and whether rats’ errors reflect the influence of pattern structure versus item associations.
One experiment (Fountain et al., 1999) sought to determine whether rats would show signs of being sensitive to the organization of nonadjacent items from interleaved subpatterns when one subpattern was a composed of a simple, repeating element and the second subpattern was either highly structured or not. For rats in the Structured (ST) subpattern condition, a 123 234 345 456 567 subpattern was interleaved with a Repeating (R) subpattern, 888 888 888 888 888, resulting in the ST-R pattern that rats were required to learn:
182838-283848-384858-485868-586878…
For rats in the Unstructured (UNST) subpattern condition, a 153 236 345 426 547 subpattern was interleaved with the same R subpattern to create the UNST-R pattern in the same manner.
Acquisition of the interleaved structured pattern (i.e., STR) was significantly faster than for the interleaved unstructured pattern (i.e., UNST-R). The unstructured pattern was generated by exchanging only two pairs of elements in the structured pattern, as described above. In so doing, however, all pair-wise associations in the interleaved patterns were maintained because all of the relocated items were preceded by “8” trials. Nevertheless, Figure 6 shows that the effects of disrupting pattern structure were apparent throughout the pattern. This was so even in the third (middle) chunk that was not altered in producing the unstructured pattern; rats found this chunk, 384858, harder to learn in the context of the UNST-R pattern than in the ST-R pattern.
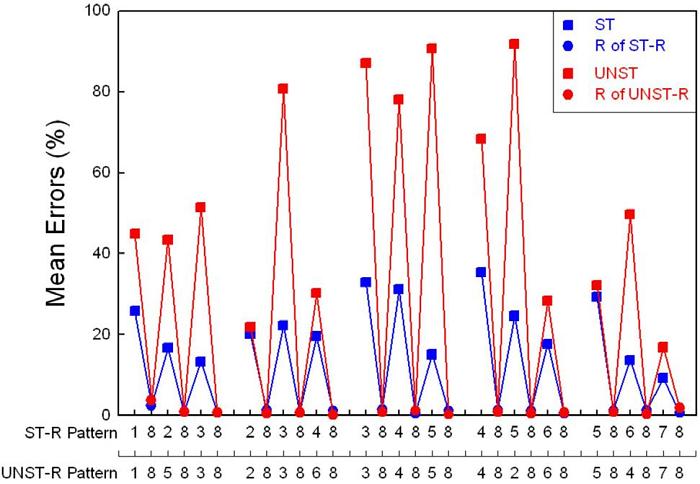
Figure 6. Group mean element-by-element errors for the interleaved structured-repeating (ST-R) and unstructured-repeating (UNST-R) patterns averaged across Week 3 of training. Note. From “Rule learning in rats: Serial tracking in interleaved patterns,” by S. B. Fountain, J. D. Rowan, and D. M. Benson, Jr., 1999, Animal Cognition, 2, p. 41-54. Copyright 1999 by Springer-Verlag. Adapted with permission.
In another experiment (Fountain & Benson, Jr., 2006), we examined the influence of pattern structure on learning interleaved patterns containing violation elements. In one group, the first interleaved subpattern was a formally simple sequence, whereas in two other groups the first subpattern was formally more complex, containing 2 or 4 violation elements, respectively. One group learned an interleaved S-S serial pattern: 1526374851627384. This interleaved pattern is based on two formally simple (S) subpatterns, 12345678 and 56781234. Both subpatterns are considered formally simple because they can be described by a single rule, namely, a “+1” rule that indicates that on successive trials the rat must choose the lever to the right of the last correct lever. In fact, the subpatterns are structurally the same, only differing in terms of where the pattern begins in the array (Lever 1 vs. Lever 5 as starting lever). This interleaved pattern was called “S-S”, to signify that it was composed of two subpatterns of simple structure. A second group learned an interleaved 2V-S serial pattern: 1526473851627384. This interleaved 2V-S pattern was composed of two subpatterns, one with 2 violation (2V) elements and the other with simple structure: 12435678 and 56781234. Note that the 2V subpattern contains two “violation” elements that break the +1 rule that describes the elements constituting the rest of this subpattern. The 2V subpattern was created by exchanging the “4” and “3” elements of the first subpattern of the S-S pattern. The second subpattern of 2V-S is identical to the second subpattern of the S-S pattern. A third group learned an interleaved 4V-S serial pattern: 1526473861527384. This interleaved 4V-S pattern was composed of two subpatterns, one with 4 violation (4V) elements and the other with simple structure: 12436578 and 56781234. The 4V subpattern was created by exchanging the “3” and “4” elements and the “5” and “6” elements of the first subpattern of the S-S pattern. The second subpattern of 4V-S is identical to the second subpattern of the S-S and 2V-S patterns.
The results showed that rats were sensitive to the relationships between elements of interleaved patterns even though the elements were not adjacent in series. Rats chunked patterns into component subpatterns, learned the “+1” rule relating nonadjacent elements of simple (S) subpatterns, and treated violation elements as structural imperfections. Evidence to support these claims for chunking and rule learning comes from 1) comparisons of pattern and subpattern acquisition rates and 2) intrusion error analyses, particularly for violation elements. Acquisition results showed that the interleaved serial pattern, S-S, composed of two subpatterns of simple structure, was learned faster than interleaved serial patterns containing violation elements, as predicted by pattern structure. Further, in each interleaved pattern, subpatterns were acquired at different rates. Even though the two S subpatterns in the interleaved serial pattern S-S were essentially identical, rats nonetheless chunked elements with respect to constituent subpattern, learning the first S subpattern faster than the second S subpattern. Similarly, with reference to the 2V-S and 4V-S interleaved patterns, the first subpatterns, which contained violation elements, were acquired faster than the second subpatterns, S in both cases. When first subpatterns are considered, the formally simple S subpattern was easier to learn than formally complex 2V and 4V subpatterns that contained violations, as predicted by rule learning theory. Taken together, these results strongly support the notion that rats were chunking patterns into their constituent subpatterns and that subpattern structure was a determinant of subpattern difficulty.
Evidence for chunking and rule learning also came from results of the intrusion error analysis. Figure 7 shows rats’ group mean element-by-element percent error rates collapsed across all days of the experiment. The top and bottom panels parse the data by first and second subpatterns of the interleaved patterns, respectively. In violation patterns (top panel), the highest-frequency errors on violation elements were responses consistent with the +1 rule describing simple subpattern structure (indicated by red circles in Figure 7 for trials where this was true). Such responses fit well with predictions of rule learning theory, but are not easily explained by common associative mechanisms of discrimination learning.
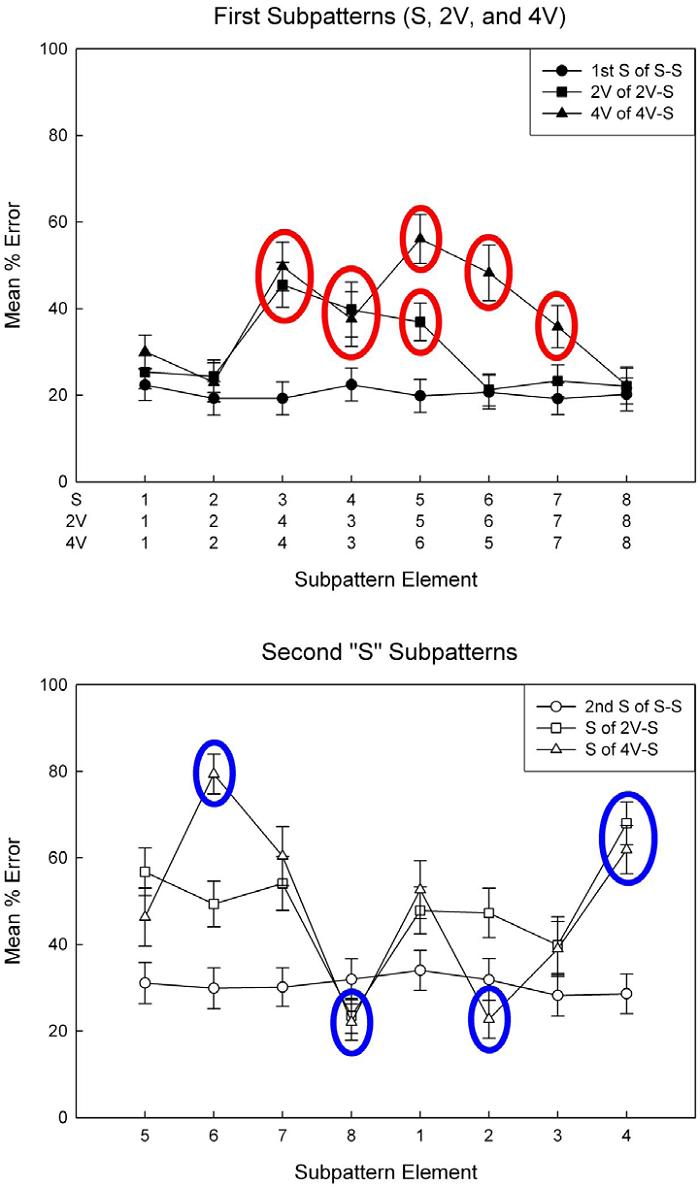
Figure 7. Rats’ group mean element-by-element percent error rates collapsed across all 5 weeks of the experiment for the S-S, 2V-S, and 4V-S interleaved patterns. The top panel shows error profiles for the first subpattern of each interleaved pattern and the bottom panel shows error profiles for the second subpattern. Red circles indicate unusually high rates of errors attributable to rule learning. Blue circles indicate unusually high or low rates of errors attributed to multiple item associations. Error bars: ± SEM. Note. From “Chunking, rule learning, and multiple item memory in rat interleaved serial pattern learning,” by S. B. Fountain and D. M. Benson, Jr., 2006, Learning and Motivation, 37, p. 95-112. Copyright 2006 by Elsevier. Adapted with permission.
If we ignore subpattern structure and treat the patterns as an undifferentiated series of events, we find strong evidence that sequential adjacent-element associations and remote associations controlled rats’ sequential choices. Several of the easiest and most difficult elements for rats to learn could be accounted for by multiple adjacent-item associations (indicated by blue circles in Figure 7 for trials where this was true). When multiple cues consistently signaled the same correct outcome, the target elements were among the easiest to learn. In contrast, when multiple cues signaled different outcomes at different points in the sequence, creating a difficult “branching” problem (Restle & Brown, 1970a; 1970b), the target elements were among the most difficult to learn due to generalization of errors across instances where the same cues predicted different outcomes. This associative view, however, cannot account for the foregoing phenomena implicating chunking and rule learning. Instead, the results taken together fit better with the idea that rats used rule learning and associative learning concurrently.
Rats appeared to learn about the formally simple rules that described the underlying interleaved structures of the sequences and governed long strings of elements. They also used associative memory of multiple items as compound cues to anticipate specific pattern elements where those cues were particularly distinctive. Thus, the behavioral evidence suggests that rats used chunking, rule learning, and interitem association learning concurrently to master these complex patterns.
SPAM and Response Sequence Learning
A natural question is whether SPAM simulations can account for the foregoing results that support the view that rat serial pattern learning of highly structured response sequences is mediated at least in part by rule induction processes. Although rats can learn the serial patterns described above to a high level of performance (no more than 10% errors on any element of the pattern), recent unpublished simulation studies indicate that SPAM failed to do so despite attempts to code sequences as series of distinct lever spatial locations or as a series of left and right turns (Kundey, Rowan, & Fountain, 2007). The insurmountable problem appears to be the highly branching nature of the serial patterns. Because SPAM depends on pairwise associations and cannot use compound or configural cues to disambiguate branching sequences, generalization is complete across instances where the same cue signals different outcomes resulting in high error rates that cannot be reduced by further “training” in SPAM. For SPAM to have any chance of simulating rats’ performance for even simple branching sequences, the model will need to be modified to encode compound or configural cues, but it is not at all clear that such a model would then be capable of simulating reward magnitude serial pattern learning or that it would produce results that simulate the foregoing data with structured response sequence learning in the octagonal chamber paradigm. Work to add compound or configural cue encoding to SPAM is currently underway.
Rule Induction and Neural Systems
Our recent research has tended to support the view described above that serial pattern learning depends on multiple concurrent learning and memory systems. Behavioral neuroscience and neurotoxicology research first reported in the 1980s has also produced evidence consistent with this idea. Specifically, early evidence indicated that more than one memory system was involved in rat serial pattern learning, at least one of which depended on the hippocampus. For example, Olton, Shapiro, and Hulse (1984) showed that fimbria- fornix lesions that effectively isolated the hippocampus produced impairments of rats’ memory for forced-choice probe elements of serial patterns that violated a simple “less than” rule learned before surgery. Similarly, Fountain, Schenk, and Annau (1985) showed that hippocampal lesions caused by the toxic organometal, trimethyltin, impaired learning for formally complex nonmonotonic serial patterns of BSR quantities, but not for formally simple monotonic patterns of BSR quantities. Impairments in rat serial pattern learning have also been observed following carbon monoxide exposure (Fountain, Raffaele, & Annau, 1986), which also differentially affects hippocampus. The foregoing results by Olton et al. and Fountain et al. fit with the putative importance of hippocampus in working, spatial, episodic, and declarative memory, and they suggest that further studies employing drugs and brain lesions targeting hippocampus might reveal relationships between cognitive processes involved in serial pattern learning and specific brain learning and memory systems.
In a recent series of studies examining the effects of drugs and brain lesions on sequential learning, we looked for converging psychobiological evidence supporting a distinction between item memory and rule induction processes in rat sequential learning. Fountain and Rowan (2000) examined the effects of the drug MK-801 on sequential learning. MK- 801 is a systemically administered drug that blocks a specific type of glutamate receptor, namely, the NMDA receptor, which plays a critical role in hippocampal learning. In blocking NMDA receptors, MK-801 also blocks a type of neuronal plasticity, known as long-term potentiation, in the hippocampus, basal ganglia, and other brain structures. It is thought that MK-801 should impair any hippocampal-dependent learning. Rats were trained on one of two patterns, one which was structurally “perfect” and a second, virtually identical to the first, but containing a single violation element as the last element of the pattern. The Perfect and Violation patterns were:
Perfect Pattern: 123-234-345-456-567-678-781-812
Violation Pattern: 123-234-345-456-567-678-781-818
As before, the digits indicate the correct order of lever choices for successive trials and dashes indicate pauses that served as phrasing cues. The last “8” item of the Violation pattern (underlined) was the violation element. Rats from one group for each pattern condition were injected with 0.0625 mg/kg MK-801 daily before training. MK-801 had little effect on learning to respond to rule-based items within chunks, but it did impair responding on the first trial of chunks and, most dramatically, for the violation element (Fountain & Rowan, 2000). Although rats showed no signs of learning to respond to the violation element, throughout the 7-day experiment they produced rule-based errors on the violation trial by responding “2” instead of “8” at the end of the sequence (Fountain & Rowan, 2000). Similar results are shown in Figure 8 from a recent unpublished master’s thesis (Smith, 2004) replication of Fountain & Rowan (2000) in an analog task with a different response and reinforcer. An octagonal chamber was fitted with nosepoke receptacles and water solenoids so that rats nosepoked for water reinforcement rather than lever pressing for BSR. Trials were signaled by receptacle lights rather lever insertion with otherwise parallel pattern training procedures. The results replicated Fountain & Rowan (2000) and provide additional evidence that MK-801 impairs NMDA-receptor-dependent processes involved in learning about chunk boundary elements and violations of pattern structure while sparing the rule induction processes necessary to induce pattern structure and extrapolate the sequence on the violation trial. Another study from Smith’s master’s thesis (2004) showed that radiofrequency lesions of dorsal that produce spatial deficits had no effects on acquisition of within-chunk elements or the violation element and caused only transient retardation of acquisition for chunk boundaries.

Figure 8. Results of a replication of Fountain and Rowan (2000). Rats’ acquisition curves for rule-governed within-chunk elements, cued chunk boundary elements, and the violation element (left-to-right panels, respectively) over 49 days of training after receiving systemic injections of either 0.0625 mg/kg MK-801 or control injections daily 30 min before training. MK-801 profoundly retarded learning (observed here as increased errors) on elements characterized as transitions between phrases of the pattern and an “exception-to-the-rule,” namely, chunk-boundary elements (Element 1 of each 3- element chunk) and the violation element (the last element of the pattern), respectively. MK-801 also produced a small and persistent effect on asymptotic levels of learning rule-governed within-chunk elements. Error bars: ± SEM.
In a later study reported in Fountain and Rowan (2000), we examined the role of NMDA-receptor-dependent processes when new serial pattern information added to old. Rats were first trained to a high criterion on a pattern consisting of the first 7 chunks of the Perfect pattern above: 123-234-345- 456-567-678-781. After rats learned the pattern, they were transferred to one of two new patterns that contained all elements of the first pattern and an additional chunk of three additional elements. The three added elements were either structurally consistent with the first pattern (viz., 812), making it a structurally Perfect pattern, or they contained a violation of the pattern structure learned in training (viz., 818), thus creating a Violation pattern. On the day of transfer, half the rats were injected with MK-801 to determine the effects of NMDA-receptor-dependent processes on rats’ ability to integrate structurally consistent or inconsistent new information with an already learned pattern.
As shown in the top panel of Figure 9, when a structurally consistent chunk was added in the Perfect pattern transfer, the effects of MK-801 were very similar to the effects of the drug on acquisition (Fountain & Rowan, 2000). That is, the drug produced a selective decrease in the animals’ accuracy on the first elements of each chunk of the original pattern, but produced virtually no change in accuracy on the remaining two elements of the 3-element chunks. The most interesting result occurred when a structurally inconsistent chunk was added in the Violation pattern transfer. As shown in the bottom panel of Figure 9, although saline control rats had difficulty responding to the new chunk, producing high error rates on the chunk boundary element and violation element of the added chunk, there was little effect on the rest of the pattern. In contrast, MK-801 dramatically disrupted performance for elements both in the new chunk to be learned and throughout the rest of the pattern (Fountain & Rowan, 2000). When this effect is compared to the effects of MK-801 in the Perfect pattern transfer, the effect can only be accounted for by the addition of the terminal violation element.
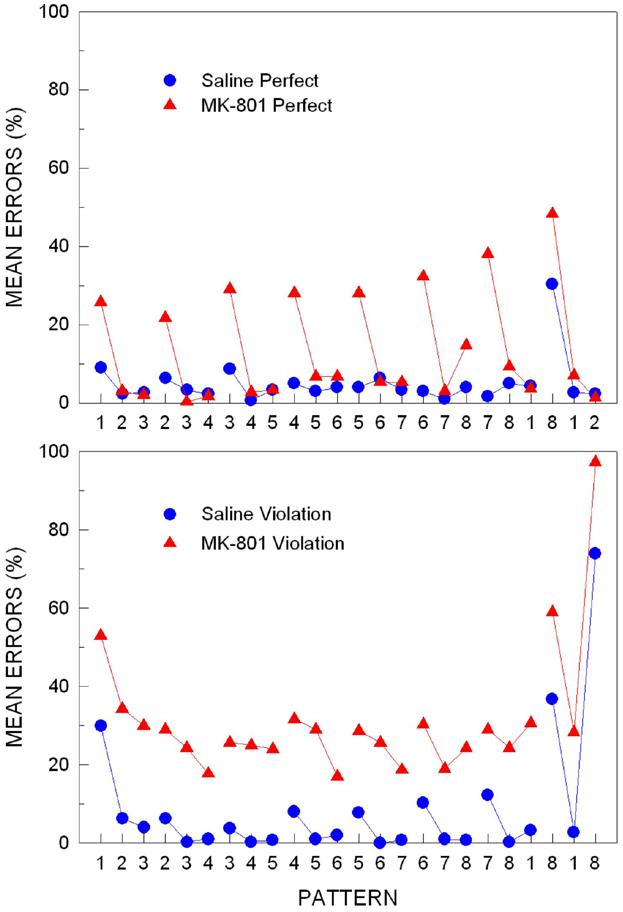
Figure 9. Rats’ mean percentage of pattern tracking errors for the perfect (top panel) and violation (bottom panel) patterns as a function of the 24 items of the patterns on the day of transfer when the eighth 3-element chunk was added to the previously learned 7-chunk pattern. On the day of transfer, rats were injected with either saline or MK-801, an NMDA receptor antagonist. Note. From “Differential impairments of rat serial-pattern learning and retention induced by MK-801, an NMDA receptor antagonist,” by S. B. Fountain and J. D. Rowan, 2000, Psychobiology, 28, p. 32-44. Copyright 2000 by Psychonomic Society. Adapted with permission.
One interpretation of these latter results is that adding new information to a pattern representation is possible under MK-801, but only if the information is consistent with pattern structure that has already been encoded. In fact, this initial evidence indicates that for rats with impairment of NMDA-receptor-dependent processes, new information that is structurally inconsistent can disrupt previously welllearned response patterns. This suggests that, in intact animals, non-NMDA-receptor-dependent systems mediate rule induction whereas NMDA-receptor-dependent processes may play a role in the successful integration of new ruleinconsistent sequential information with already encoded information about pattern structure. Under MK-801, rats were able to add a rule-consistent chunk to their already learned pattern with relatively little difficulty, but not a rule-inconsistent chunk.
Muscarinic acetylcholine systems have been implicated in cognitive dysfunction in aging and Alzheimer’s disease and play a role in cortical, hippocampal, and subcortical brain functions (Altavista, Bentivoglio, Crociani, Rossi, & Albanese, 1988; Bartus, Dean, III, Beer, & Lippa, 1982; Ikonen, McMahan, Gallagher, Eichenbaum, & Tanila, 2002; Maddux, Kerfoot, Chatterjee, & Holland, 2007; Sarter, 2007). In a series of studies from a recently-defended master’s thesis, Chenoweth (2007) examined the effects of atropine, a muscarinic cholinergic antagonist, on serial pattern learning in the same paradigm as that used to study effects of MK-801. She showed that atropine produces effects in acquisition and retention similar to those produced by MK-801. For now, we do not understand the biological basis for the correspondence between the effects atropine, a cholingergic antagonist, and MK-801, a glutamatergic NMDA receptor antagonist, but studies to elucidate this relationship are ongoing.
The picture that is emerging from our psychobiological research is complex, but evidence strongly suggests that within- chunk elements, chunk-boundary elements, and violation elements are likely to be differentially sensitive to manipulations of different neurotransmitter and neuroanatomical systems. The results to date fit well with the view that sequential learning depends on multiple concurrent processes and with the thesis of this paper, namely, that rats use rule induction processes in addition to and concurrent with putative associative processes in sequential learning (cf., Fountain, 2006; Fountain & Benson, Jr., 2006; Fountain & Rowan, 2000; Fountain et al., 2007; Wallace et al., in press).
Pattern Structure, Compound Associations, and Relative Rate of Acquisition
One potential objection to the foregoing interpretation of our results is the idea that the drug and lesion effects we observed might be simply a function of task difficulty. That is, perhaps drugs and lesions differentially impaired learning for chunk-boundary and violation elements because these elements are significantly more difficult to learn than within- chunk elements. One retort to this objection is that the observed drug and lesion effects appear to be permanent and profound, not simply graded as a function of task difficulty. Another response is that they demonstrate both the absence of the process involved in using cues to anticipate future sequential events and the sparing of rule induction processes. However, a particular interesting new result from our lab to be discussed next suggests that drug- and lesion-induced deficits are not related to greater task difficulty at all.Muller (2006), in an effort to examine the role of pattern structure in determining acquisition rate, conducted a 3-group study as part of her dissertation in my lab. She examined the acquisition of within-chunk elements, chunk-boundary elements, and a single violation element in three patterns with analogous 2-level hierarchical structure but with chunks of different length:
3-element chunks: 123-234-345-456-567-678-781-818
4-element chunks: 1234-3456-5678-7818
5-element chunks: 12345-45678-78121
During the first few days of training, rats worked through a program of increasing numbers of patterns until they reached the target of 50 patterns per day. Rats were then trained on 50 patterns per day until they completed acquisition training. In the left panel of Figure 10, acquisition data are plotted as they traditionally are in both human and animal serial learning papers as group mean day-by-day scores. In this case, data were pooled across groups because there were no significant differences between groups. Pattern hierarchical structure was a better predictor of pattern difficulty overall and for specific element types than was pattern length, chunk length, the number of chunks, or the number of chunk boundaries. The results fit well with those reported earlier by Fountain and Rowan (1995a) showing the importance of hierarchical structure as a determinant of sequential learning.
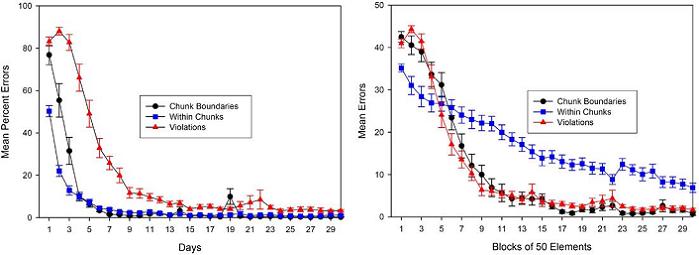
Figure 10. Rats’ acquisition curves (plotted as decreasing errors over days) for rule-governed within-chunk elements, cued chunk boundary elements, and the violation element over 30 days of training. Left panel: Data plotted traditionally as daily means for each element type. Data presented in this way suggest that within-chunk elements were the easiest to learn, the violation element were the most difficult, and chunk boundaries were intermediate in difficulty. Right panel: The same data plotted as a function of blocks of 50 instances of each element type, thus equating for experience with each type. Data presented in this way suggest that within-chunk elements were the most difficult to learn and that transitions between phrases of the pattern and an “exception-to-the-rule,” namely, chunk-boundary and violation elements, respectively, were learned at a faster rate than within-chunk elements with no significant differences between chunk-boundary and violation elements. Error bars: ± SEM.
In addition, viewed from this perspective, the data support the common claim that pattern structural changes, like transitions between phrases at chunk boundaries, and “exceptions structurally simpler rule-based information (Fountain, 1990; Fountain & Rowan, 1995a; 1995b; Jones, 1974; Kotovsky & Simon, 1973; Restle & Brown, 1970a). One consistent observation in both human and animal sequential learning is that the kinds of errors subjects make on chunk-boundary and violation elements are frequently consistent with overextensions of the pattern’s inherent base structure, such as when rats frequently make a “4” response on a chunkboundary trial after a 1-2-3 chunk or make a rule-consistent “2” response rather than the violation “8” response at the end of the 3-element-chunks pattern in this experiment (cf. Fountain & Rowan, 1995a; 1995b). This suggests that the base rules of a pattern are learned faster than chunk-boundary and violation elements. However, it should be noted that the data supporting the claim that transitions between phrases (chunk boundaries) and “exceptions-to-the-rule” (violation elements) are more difficult to learn than rule-governed within-chunk responses are confounded by the fact that chunk boundaries and violation elements are by definition less frequent than rule-governed within-chunk elements. As it turns out, the most frequent rules actually determine the interpretation of the structure that is perceived and encoded, so it is no surprise that transitions between phrases of a pattern and “exceptions-to-the-rule” are less frequent events in any sequence perceived as having a pattern structure.
However, it is possible to plot the data in the left panel of Figure 10 not in terms of daily mean errors, but as a function of the number of times rats encountered each type of pattern element (viz., within-chunk vs. chunk-boundary vs. violation elements). In the right panel of Figure 10, the data from the left panel are as a function of blocks of 50 instances of each element type, thus equating for experience with each type. Data presented in this way suggest that within-chunk elements were the most difficult to learn. Transitions between phrases of the pattern and an “exception-to-the-rule,” namely, chunk-boundaries and violation elements, respectively, were learned at a faster rate than within-chunk elements with no significant differences between chunk-boundary and violation elements. One might argue that such an analysis is difficult to interpret because of the large differences in the relative timing and spacing of the events being pooled for analysis, but this idea would likely lead one to expect the slowest learning in widely spaced chunk-boundary and violation elements, not faster learning relative to closely spaced within-chunk elements as we observed. Muller’s result does not refute the idea that rats and humans are sensitive to and learn about pattern structure, but it does suggest that learning pattern rules may be more difficult compared to discrimination learning than previously thought. This outcome also bears on interpreting our preliminary drug and lesion studies mentioned above, some of which show larger deficits for chunk-boundary and violation elements than for within-chunk elements. From the traditional perspective, this outcome might suggest a drug or lesion effect that depends on task difficulty, but this latter conclusion would not necessarily be supported by data from the right panel of Figure 10 that indicate that within-chunk elements are actually learned slower, not faster, than other element types.
It has often been stated that pattern abstraction leads to more efficient mnemonic representations. Some have used this idea to justify why animals might have developed abstract cognitive processes or why animals might employ them under appropriate circumstances. The results of this study suggest that whereas pattern structure is an important determinant of pattern learning, it does not necessarily follow that pattern perception and encoding is easier or faster than S-R learning, pairwise association, compound or configural cue learning, encoding occasion setters, encoding “multiple item memory,” or other forms of associative learning.
Pattern Structure, Rule Induction, and the Organization of Behavior
What role do pattern structure and rule induction play in the organization of behavior? The foregoing discussion resonates with research from behavioral neuroscience and related fields that has found evidence for more than one process and more than one brain area mediating human and nonhuman sequential learning. Nissen’s broadly influential work on brain correlates of human learning in her serial reaction time (SRT) task has supported the idea that serial learning is subserved by at least two dissociable learning systems (Knopman & Nissen, 1991; Knopman & Nissen, 1987; Nissen, Knopman, & Schacter, 1987). Work from Graybiel’s lab indicates that the basal ganglia are critical for both cognitive and motor aspects of sequential learning (e.g., Canales & Graybiel, 2000; Fujii & Graybiel, 2003; Graybiel, 1997; 1998; 2000; Jog, Kubota, Connolly, Hillegaart, & Graybiel, 1999; Saka, Goodrich, Harlan, Madras, & Graybiel, 2004) and likely also play a role in schizophrenia, Tourette’s syndrome, and obsessive-compulsive disorder (e.g., Graybiel, 1997; Graybiel & Canales, 2001; Graybiel & Rauch, 2000; Holt et al., 1999; Saka & Graybiel, 2003). Lesions of hippocampus and medial caudoputamen in rats produce a double dissociation of processes in sequential learning (DeCoteau & Kesner, 2000), and hippocampal lesions have also been shown to cause deficits in rats’ ability to disambiguate serial patterns (Agster, Fortin, & Eichenbaum, 2002). Willingham’s recent model of human sequential learning and performance posits dissociable perceptual-motor, strategic, and dynamic processes involving dorsolateral frontal cortex, premotor cortex, basal ganglia and other subcortical structures, and spinal systems, respectively (Bischoff-Grethe, Goedert, Willingham, & Grafton, 2004; Willingham, 1998; 1999). Growing evidence indicates that sequential learning recruits multiple dissociable cognitive and neural systems concurrently, yet the behavioral and neural processes that subserve it have not been definitively identified and properly characterized. For example, the SRT task, which has many similarities to our method, has become widely adopted in cognitive neuroscience, behavioral neuroscience, and clinical research for imaging, animal drug and lesion studies, and for studying cognitive deficits in patient populations. Whether or not rule learning, chunking, and other “patterning” effects (cf. Koch & Hoffmann, 2000) can be observed in this paradigm at all is currently a matter of debate. The research reported in this paper supports claims that rats routinely respond to pattern structure and rule induction processes in a wide variety of sequential learning problems. This suggests that rule induction may play a more central role in response sequence learning than is generally recognized.
References
Agster, K. L., Fortin, N. J., & Eichenbaum, H. (2002). The hippocampus and disambiguation of overlapping sequences. Journal of Neuroscience, 22, 5760-5768.
Altavista, M. C., Bentivoglio, A. R., Crociani, P., Rossi, P., & Albanese, A. (1988). Age-dependent loss of cholinergic neurones in basal ganglia of rats. Brain Research, 455, 177-181.
Bartus, R. T., Dean, R. L., III, Beer, B., & Lippa, A. S. (1982). The cholinergic hypothesis of geriatric memory dysfunction. Science, 217, 408-414.
Bischoff-Grethe, A., Goedert, K. M., Willingham, D. T., & Grafton, S. T. (2004). Neural substrates of response-based sequence learning using fMRI. 16, 127-138.
Blumberg, M. S., & Wasserman, E. A. (1995). Animal mind and the argument from design. American Psychologist, 50, 133-144.
Bruner, J. S. (1957). Going beyond the information given. In J. S. Bruner, E. Brunswik, L. Festinger, F. Heider, K. F. Muenzinger, C. E. Osgood, & D. Rapaport (Eds.), Contemporary approaches to cognition (pp. 41-69). Cambridge, MA: Harvard University Press.
Canales, J. J., & Graybiel, A. M. (2000). A measure of striatal function predicts motor stereotypy. 3, 377-383.
Capaldi, E. J., & Molina, P. (1979). Element discriminability as a determinant of serial-pattern learning. Animal Learning & Behavior, 7, 318-322.
Capaldi, E. J., Verry, D. R., & Davidson, T. (1980). Memory, serial anticipation pattern learning, and transfer in rats. Animal Learning & Behavior, 8, 575-585.
Chenoweth, A. M. (2007). The effects of muscarinic cholinergic blockade on rat serial pattern learning and retention. Unpublished master’s thesis. Kent State University, Kent, OH.
Church, R. M. (1997). Quantitative models of animal learning and cognition. Journal of Experimental Psychology: Animal Behavior Processes, 23, 379-389.
Church, R. M. (2001). A Turing test for computational and associative theories of learning. Current Directions in Psychological Science, 10, 132-136.
DeCoteau, W. E., & Kesner, R. P. (2000). A double dissociation between the rat hippocampus and medial caudoputamen in processing two forms of knowledge. Behavioral Neuroscience, 114, 1096-1108.
Fountain, S. B. (1990). Rule abstraction, item memory, and chunking in rat serial-pattern tracking. Journal of Experimental Psychology: Animal Behavior Processes, 16, 96-105.
Fountain, S. B. (2006). The structure of sequential behavior. In E. A. Wasserman & T. R. Zentall (Eds.), Comparative Cognition: Experimental Explorations of Animal Intelligence (pp. 439-458). Oxford: Oxford University Press.
Fountain, S. B., & Annau, Z. (1984). Chunking, sorting, and rule-learning from serial patterns of brain-stimulation reward by rats. Animal Learning & Behavior, 12, 265- 274.
Fountain, S. B., Benson, A. M., & Wallace, D. G. (2000). Number, but not rhythmicity, of temporal cues determines phrasing effects in rat serial-pattern learning. Learning and Motivation, 31, 301-322.
Fountain, S. B., & Benson, D. M., Jr. (2006). Chunking, rule learning, and multiple item memory in rat interleaved serial pattern learning. Learning and Motivation, 37, 95- 112.
Fountain, S. B., & Hulse, S. H. (1981). Extrapolation of serial stimulus patterns by rats. Animal Learning & Behavior, 9, 381-384.
Fountain, S. B., Raffaele, K. C., & Annau, Z. (1986). Behavioral consequences of intraperitoneal carbon monoxide administration in rats. Toxicology and Applied Pharmacology, 83, 546-555.
Fountain, S. B., & Rowan, J. D. (1995a). Coding of hierarchical versus linear pattern structure in rats and humans. Journal of Experimental Psychology: Animal Behavior Processes, 21, 187-202.
Fountain, S. B., & Rowan, J. D. (1995b). Sensitivity to violations of “run” and “trill” structures in rat serialpattern learning. Journal of Experimental Psychology: Animal Behavior Processes, 21, 78-81.
Fountain, S. B., & Rowan, J. D. (2000). Differential impairments of rat serial-pattern learning and retention induced by MK-801, an NMDA receptor antagonist. Psychobiology, 28, 32-44.
Fountain, S. B., Rowan, J. D., & Benson, D. M., Jr. (1999). Rule learning in rats: Serial tracking in interleaved patterns. Animal Cognition, 2, 41-54.
Fountain, S. B., Rowan, J. D., & Carman, H. M. (2007). Encoding structural ambiguity in rat serial pattern learning: The role of phrasing. International Journal of Comparative Psychology, 20, 25-34.
Fountain, S. B., Rowan, J. D., Muller, M. D., Smith, D. P. A., Chenoweth, A. M., & Wallace, D. G. (2006). Sequence production paradigms for exploring the organization of sequential behavior. In M. J. Anderson (Ed.), (pp. 245- 260). Hauppauge, NY: Nova Science.
Fountain, S. B., Schenk, D. E., & Annau, Z. (1985). Serialpattern- learning processes dissociated by trimethyltin exposure in rats. Physiological Psychology, 13, 53-62.
Fujii, N., & Graybiel, A. M. (2003). Representation of action sequence boundaries by macaque prefrontal cortical neurons. Science, 301, 1246-1249.
Gallistel, C. R. (1995). The replacement of general-purpose theories with adaptive specializations. In M. S. Gazzaniga (Ed.), The cognitive neurosciences (pp. 1255-1267). Cambridge, MA: MIT Press.
Graybiel, A. M. (1997). The basal ganglia and cognitive pattern generators. 23, 459-469.
Graybiel, A. M. (1998). The basal ganglia and chunking of action repertoires. Neurobiol. Learn. Mem., 70, 119-136.
Graybiel, A. M. (2000). The basal ganglia. 10, R509-R511.
Graybiel, A. M., & Canales, J. J. (2001). The neurobiology of repetitive behaviors: clues to the neurobiology of Tourette syndrome. 85, 123-131.
Graybiel, A. M., & Rauch, S. L. (2000). Toward a neurobiology of obsessive-compulsive disorder. Neuron, 28, 343-347.
Haggbloom, S. J. (1985). Serial learning and transfer in rats: effects of changes in stimulus-stimulus associations, pattern structure, and serial position information. Animal Learning & Behavior, 13, 370-374.
Haggbloom, S. J., & Brooks, D. M. (1985). Serial anticipation and pattern extrapolation in rats as a function of element discriminability. Animal Learning & Behavior, 13, 303- 308.
Holt, D. J., Herman, M. M., Hyde, T. M., Kleinman, J. E., Sinton, C. M., German, D. C. et al. (1999). Evidence for a deficit in cholinergic interneurons in the striatum in schizophrenia. Neuroscience, 94, 21-31.
Hulse, S. H. (1973). Patterned reinforcement. In G. Bower (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 7) (pp. 313-362). New York: Academic Press.
Hulse, S. H. (1978). Cognitive structure and serial pattern learning by animals. In S. H. Hulse, H. Fowler, & W. K. Honig (Eds.), Cognitive processes in animal behavior (1 ed., pp. 311-340). Hillsdale, NJ: Erlbaum.
Hulse, S. H., & Dorsky, N. P. (1977). Structural complexity as a determinant of serial pattern learning. Learning and Motivation, 8, 488-506.
Hulse, S. H., & Dorsky, N. P. (1979). Serial pattern learning by rats: Transfer of a formally defined stimulus relationship and the significance of nonreinforcement. Animal Learning & Behavior, 7, 211-220.
Ikonen, S., McMahan, R., Gallagher, M., Eichenbaum, H., & Tanila, H. (2002). Cholinergic system regulation of spatial representation by the hippocampus. Hippocampus, 12, 386-397.
Jog, M. S., Kubota, Y., Connolly, C. I., Hillegaart, V., & Graybiel, A. M. (1999). Building neural representations of habits. Science, 286, 1745-1749.
Jones, M. R. (1974). Cognitive representations of serial patterns. In B. Kantowitz (Ed.), Human information processing: Tutorials in performance and cognition (1 ed.), Hillsdale,NJ: Erlbaum.
Knopman, D., & Nissen, M. J. (1991). Procedural learning is impaired in Huntington’s disease: Evidence from the serial reaction time task. Neuropsychologia, 29, 245-254.
Knopman, D. S., & Nissen, M. J. (1987). Implicit learning in patients with probable Alzheimer’s disease. Neurology, 37, 784-788.
Koch, I., & Hoffmann, J. (2000). Patterns, chunks, and hierarchies in serial reaction-time tasks. Psychological Research, 63, 22-35.
Kotovsky, K., & Simon, H. A. (1973). Empirical tests of a theory of human acquisition of concepts for sequential patterns. Cognitive Psychology, 4, 399-424.
Kundey, S. M. A., Rowan, J. D., and Fountain, S. B. (2007, March). Some limitations of the Sequential Pairwise Associative Memory (SPAM) model of rat serial pattern learning. Poster presented at the annual meeting of the International Conference on Comparative Cognition, Melbourne, FL.
Lashley, K. S. (1951). The problem of serial order in behavior. In L. A. Jeffress (Ed.), Cerebral mechanisms in behavior (1 ed., pp. 112-146). New York: Wiley.
Maddux, J. M., Kerfoot, E. C., Chatterjee, S., & Holland, P. C. (2007). Dissociation of attention in learning and action: Effects of lesions of the amygdala central nucleus, medial prefrontal cortex, and posterior parietal cortex. Behavioral Neuroscience, 121, 63-79.
Metcalfe Eich, J. (1982). A composite holographic associative recall model. Psychological Review, 89, 627-661.
Metcalfe, J. (1990). Composite holographic associative recall model (CHARM) and blended memories in eyewitness testimony. Journal of Experimental Psychology: General, 119, 145-160.
Metcalfe, J. (1993). Novelty monitoring, metacognition, and control in a composite holographic associative recall model: Implications for Korsakoff amnesia.Psychological Review, 100, 3-22.
Muller, M. D. (2006). Serial pattern learning in rats: Identifying the processes underlying three patterns. Unpublished doctoral dissertation, Kent State University, Kent, OH.
Murdock, B. B. (1982). A theory for the storage and retrieval of item and associative information. Psychological Review, 89, 609-626.
Murdock, B. B. (1983). A distributed memory model for serial-order information. Psychological Review, 90, 316- 336.
Murdock, B. B. (1985). Convolution and matrix systems: A reply to Pike. Psychological Review, 92, 130-132.
Murdock, B. B. (1992). Serial organization in a distributed memory model. In A. F. Healy, S. M. Kosslyn, & R. M. Shiffrin (Eds.), (pp. 201-225). Hillsdale, NJ: Lawrence Erlbaum.
Murdock, B. B. (1995). Developing TODAM: Three models for serial-order information. Memory and Cognition, 23, 631-645.
Neath, I., & Capaldi, E. J. (1996). A “random-walk” simulation model of multiple-pattern learning in a radial arm maze. Animal Learning & Behavior, 24, 206-210.
Newell, A., & Simon, H. A. (1961). Computer simulation of human thinking. Science, 134, 2011-2017.
Nissen, M. J., Knopman, D. S., & Schacter, D. L. (1987). Neurochemical dissociation of memory systems. Neurology, 37, 789-794.
Olton, D. S., Shapiro, M. L., & Hulse, S. H. (1984). Working memory and serial patterns. In H. L. Roitblat, T. G. Bever, & H. S. Terrace (Eds.), (pp. 171-182). Hillsdale, NJ: Lawrence Erlbaum Associates.
Restle, F. & Brown, E. R. (1970a). Organization of serial pattern learning. In G. H. Bower (Ed.), Psychology of learning and motivation (1 ed.), New York: Academic Press.
Restle, F., & Brown, E. R. (1970b). Serial pattern learning. Journal of Experimental Psychology, 83, 120-125.
Roitblat, H. L. (2002). The structure of events. In S. B. Fountain, M. Bunsey, J. H. Danks, & M. K. McBeath (Eds.), (pp. 249-268). Boston, MA: Kluwer Academic.
Roitblat, H. L., & von Fersen, L. (1992). Comparative cognition: Representations and processes in learning and memory. Annual Review of Psychology, 43, 671-710.
Saka, E., Goodrich, C., Harlan, P., Madras, B. K., & Graybiel, A. M. (2004). Repetitive behaviors in monkeys are linked to specific striatal activation patterns. Journal of Neuroscience, 24, 7557-7565.
Saka, E., & Graybiel, A. M. (2003). Pathophysiology of Tourette’s syndrome: striatal pathways revisited. S15- S19.
Sarter, M. (2007). Cholinergic control of attention to cues guiding established performance versus learning: Theoretical comment on Maddux, Kerfoot, Chatterjee, and Holland (2007). Behavioral Neuroscience, 121, 233- 235.
Simon, H. A., & Kotovsky, K. (1963). Human acquisition of concepts for sequential patterns. Psychological Review, 70, 534-546.
Smith, D. P. A. (2004). The effects of MK-801 and hippocampal lesions on serial pattern learning. Unpublished master’s thesis, Kent State University, Kent, OH.
Stempowski, N. K., Carman, H. M., & Fountain, S. B. (1999). Temporal phrasing and overshadowing in rat serial-pattern learning. Learning and Motivation, 30, 74-100.
Wallace, D. G., & Fountain, S. B. (2002). What is learned in sequential learning? An associative model of reward magnitude serial-pattern learning. Journal of Experimental Psychology: Animal Behavior Processes, 28, 43-63.
Wallace, D. G., & Fountain, S. B. (2003). An associative model of rat serial pattern learning in 3-element sequences. Quarterly Journal of Experimental Psychology: Comparative and Physiological Psychology, 56B, 301- 320.
Wallace, D. G., Lewis, C. F., Fountain, S. B., & Block, C. H. (1999). Rat “rule induction” can be modeled by a neural network with supervised learning. Society for Neuroscience Abstracts, 25, 85.
Wallace, D. G., Rowan, J. D., & Fountain, S. B. (2007). Determinants of phrasing effects in rat serial pattern learning. Animal Cognition, DOI 10.1007/s10071-007- 0110-7.
Willingham, D. B. (1998). A neuropsychological theory of motor skill learning. Psychological Review, 105, 558- 584.
Willingham, D. B. (1999). The neural basis of motor-skill learning. Current Directions in Psychological Science, 8, 178-182.