 Forgetting from Short-Term Memory in Delayed Matching to Sample: A Reinforcement Context Model
Forgetting from Short-Term Memory in Delayed Matching to Sample: A Reinforcement Context Model
K. Geoffrey White and Glenn S. Brown
University of Otago, New Zealand
Reading Options:
Continue reading below, or:
Read/Download PDF | Add to Endnote
Abstract
Short-term memory in nonhuman animals is typically studied in delayed matching to sample, with variation in the retention interval or delay between the to-be-remembered sample and subsequently presented choice or comparison stimuli. The forgetting function, which relates the systematic decrease in discriminability to increasing delay, is well described by an exponential in the square root of time, with an intercept and slope that vary systematically with different conditions, such as sample-stimulus disparity, retention-interval conditions, and reward parameters. We argue that the rewards for accurate matching are relative to the reinforcement context, which includes rewards Ro for extraneous or other behaviors. Forgetting results from competition between Ro and rewards for the delayed matching task. We suggest that Ro acts to shift attention from the memory task to extraneous behavior, and that Ro grows as a linear function of time in the retention interval. By incorporating these assumptions in the model proposed by White and Wixted (1999), we accurately predict the time course of forgetting under a variety of different conditions for delayed matching.
Keywords: forgetting, reinforcement, interference, extraneous behavior, short-term memory, delayed matching, pigeon
Author Note: An earlier version was presented to the Society for Quantitative Analysis of Behavior, Phoenix, Arizona, 2009. We thank our lab group and Sara-Lee Illingworth for their contribution to our own experiments reviewed here. Address correspondence to geoff.white@otago.ac.nz.
More than fifty years ago, Peterson and Peterson (1959) and J. Brown (1958) demonstrated that people quickly forget unfamiliar combinations of letters (three-letter trigrams) if they are prevented from rehearsing them. In their experiments, recall accuracy systematically fell as the retention interval lengthened. This result provided the first empirical evidence for a short-term memory process in which a memory trace decays in a matter of seconds. This classic result has been confirmed many times in research with humans, and with a variety of to-be-remembered stimuli (Baddeley, 1997). The result supports a major theoretical account of forgetting: that forgetting occurs via a passive decay of memory traces over time.
In another landmark study published at the same time as the Petersons’, Blough (1959) demonstrated short-term forgetting in pigeons. Blough’s pigeons worked for food in a delayed matching-to-sample task. In this task, a to-be-remembered sample stimulus was presented at the beginning of each trial. After a retention interval lasting up to 5 or 10 s, the pigeon chose one of two comparison stimuli. Correct choices that matched the prior sample were rewarded with food. Blough observed the pigeons’ behavior during the retention interval. Pigeons that developed different behavior patterns during the retention interval for each sample (e.g., bobbing up and down for one sample and a different behavior for the other sample, as though rehearsing) were able to recall the sample with very high accuracy, even after 10 s. Memory accuracy for pigeons without such rehearsal-like behaviors, however, declined rapidly with increasing delay, just as in the studies with humans. Like theories of human forgetting, the main theory of forgetting in nonhuman animals assumed that, unless memory traces are maintained by rehearsal (Grant, 1981), traces decay with time (Roberts, 1972).
Decay theories of human short-term memory, compared to alternative theories, continue to be hotly debated (Lewandowsky, Oberauer, & Brown, 2009; Nairne, 2002; Portrat, Barrouillet, & Camos, 2008; Surprenant & Neath, 2009; White, 2012). Earlier, McGeoch (1932) argued that the main mechanism to account for forgetting is interference (Roediger, Weinstein, & Agarwal, 2010).
In the present paper, we propose a theory for forgetting from short-term memory in nonhuman animals that generally follows the interference principle. Unlike McGeogh’s original idea of response competition as the source of interference, our theory is based on reinforcement competition. This notion stems from Herrnstein’s (1961, 1970) matching law. According to this law, the strength of a response is predicted by the rewards it produces, relative to rewards for alternative behaviors. That is, the effectiveness of rewards for a behavior of interest is relative to the reinforcement context provided by all sources of reinforcement. Thus the rewards for alternative, or other, behaviors, Ro, compete with the rewards for completing or attending to the main task. We outline our theory in more detail below, but we first explain the two main characteristics of a forgetting function that the theory must account for. Descriptively, these are the intercept and slope of the forgetting function relating memory performance to the passage of time.
Forgetting Functions
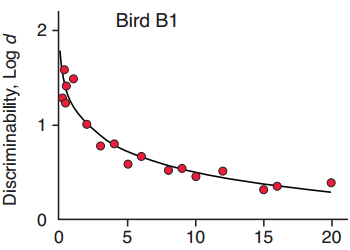
Figure 1. The exponential in the square root of time, y = a·exp(b·?t), fitted to data for the pigeon, Bird B1, in one condition reported by Sargisson & White (2003).
Over the fifty or so years since the seminal work, studies with a wide range of species have explored short-term forgetting functions (Rubin & Wenzel, 1996; White, 2001, 2013). Forgetting typically follows a systematically decreasing function in which performance gradually decreases as the retention interval lengthens. The form of the function could be logarithmic (Woodworth & Shlosberg, 1954), power (Wixted & Carpenter, 2007; Wixted & Ebbesen, 1991), exponential (White, 1985), hyperbolic (Staddon, 1983), or exponential in the square root of time (Harper & White, 1997; White, 2001). These were among the best-fitting functions of the large number that Rubin and Wenzel (1996) fitted to data from over 200 studies with both humans and nonhumans. The common characteristic of all their best-fitting functions is that accuracy decreases monotonically as time since the to-be-remembered event elapses. With the best-fitting functions such as the power and exponential in the square root of time (White, 2001), forgetting is slower at longer retention intervals, consistent with what might be expected if memories consolidate with time (Wixted, 2004, 2010). In the present paper, we use the exponential in the square root of time, that is, y = a·exp(b·?t), because it does an excellent job of fitting data from a wide range of studies using the delayed matching-to-sample task (see White, 2013, for review). To illustrate, in Figure 1, this function was fitted to data for a pigeon trained in a delayed matching-to-sample task with 18 different delays arranged in an arithmetic progression (Sargisson & White, 2003). Five sets of different delays were run in rotations of five daily sessions over a large number of total sessions, with a few overlapping delays across sets. The fitted function (solid line) has an intercept of a = 1.79, has a slope of b = .04, and accounted for 92 percent of the variance in the data. In the present paper, this equation is used to describe an entire forgetting function—the function relating discriminability to retention-interval duration. An important requirement for our model is the ability to predict differences in both intercept and slope of the forgetting functions over a range of conditions. The examples selected below usefully illustrate such changes, but we do not attempt an exhaustive review of delayed matching studies.
In the examples that follow, we use a measure of discriminability to describe the pigeon’s accuracy in delayed matching. As it happens, conclusions drawn based on the discriminability measure do not differ from those based on the more usual measure, percent correct (White, 1985). The discriminability measure, however, like d’ in signal detection theory, has the advantage that it is bias-free, and varies on a dimension that has equalinterval properties and has no upper bound to create ceiling effects (White, 2001). The discriminability measure used here, log d, was derived by Davison and Tustin (1978) and is the log (base 10) of the ratio of correct to error responses. For sample stimuli S1 and S2, log d = 0.5 log10 [(correct responses following S1 × correct responses following S2)/(errors following S1 × errors following S2)].
Reinforcement Context
During the retention interval of a short-term memory task, including delayed matching to sample, various activities or events may intervene to interfere with remembering the sample stimuli or to-be-remembered items. Experimentally introduced interference in a human list-learning task might include the learning of another list, or the introduction of competing (‘concurrent’) tasks at encoding or retrieval. Wixted (2004, 2010) argued that such interference in everyday remembering is nonspecific in that the intervening event does not have to be specifically related to the to-be-remembered items. In delayed matching to sample, the pigeon engages in extraneous or other behaviors during the retention interval. When the experimental chamber is dark, these may be restricted to wing flapping or pacing for a pigeon (a visual animal), and when the chamber is illuminated, the pigeon will peck at grains of wheat spilt from the hopper, or at screws or small marks on the chamber walls. In Blough’s (1959) seminal study, the behaviors during the retention interval were carefully recorded and for some pigeons seemed to be correlated with performance on the memory task. More generally, illuminating the chamber during the retention interval creates conditions for retroactive interference, and matching accuracy is adversely affected (Roberts & Grant, 1978; Zentall, 1973). For the present model, we assume that other behaviors extraneous to the task of remembering occur throughout the retention interval, whatever they are, and that they are rewarded by extraneous or other reinforcers, Ro, following Herrnstein’s (1970) supposition of extraneous reinforcement. In general, Ro is a hypothetical entity, although it could be supplemented by experimenter-defined extraneous reinforcement, as Brown and White (2005b) did when they reinforced key pecking on a variable-interval schedule during the retention interval (see below). Ro is part of the reinforcement context. If the reinforcement context includes just the rewards R for a target behavior B, and Ro, which rewards other behavior Bo, Herrnstein’s (1970) application of the matching law predicts the relative strength of the target behavior from B/(B + Bo) = R/(R + Ro). The effect of R is relative to the total reinforcement context R + Ro.
A Modified White-Wixted Model
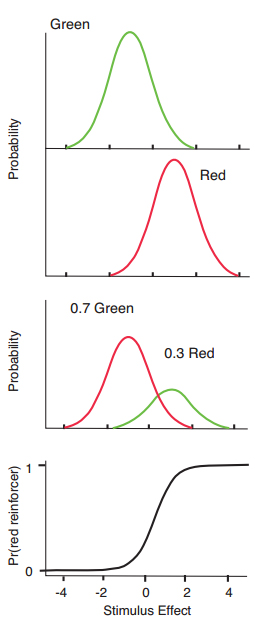
Figure 2. Hypothetical distributions of stimulus effect for green and red samples (top two panels), and reward probability distributions (third panel) that result from multiplying them by arranged reward probabilities (0.7 and 0.3 for correct green and red choices respectively, in the example), and the distribution of relative reward probability for correct red choices on the stimulus effect dimension (bottom panel).
White and Wixted (1999) described a model for delayed matching performance that was reminiscent of signal detection theory, but that based the decision rule on the matching law. Like signal detection theory, the model assumes that the sample stimuli (for example, green and red hues) are associated with Thurstone’s (1927) discriminal distributions along a dimension of stimulus value or stimulus effect (Figure 2, top two panels). Unlike signal detection theory, however, in the present model the individual has no knowledge of these distributions. Instead, the individual’s knowledge is about distributions of relative reinforcement along the dimension of stimulus effect. The reinforcement distributions are derived (in the model) by multiplying the stimulus effect distribution in the top panel by the probability of reinforcement for correct red or green choices. The third panel in Figure 2 shows the result for an example where reinforcement probabilities were 0.7 and 0.3 for correct choices of green and red comparison stimuli respectively. The bottom panel of Figure 2 shows the distribution of the proportion of rewards for correct choices of red as a function of stimulus value.
For the present modeling, the stimulus effect distributions were set up using the NORMDIST function in Excel, and reinforcement distributions were generated by multiplying the normal distributions by reinforcement probabilities (1.0 in most cases). The discriminal distributions are set apart by D z-units, and for standard deviations of the distributions set at 1.0, the only free parameter in the model is D. The model works in the following way. On each trial, the red or green sample is randomly selected, and a value (i) is sampled on the stimulus effect dimension (in relation to the relevant normal distribution). That value is associated with a specific ratio (R1i / R2i) or proportion of rewards that have been gained in the past. Given the stimulus value i, the individual makes a choice response B1i or B2i to comparison stimuli 1 and 2, according to the matching law. That is, at stimulus value i, B1i/B2i = (R1i)/(R2i). By summing choice responses B1i and B2i across all values of stimulus effect, and also the rewards they produce (which depend on the reward probabilities), a matrix is generated, which gives B1 and B2 choices following S1 and S2 samples, and also the rewards they obtain. This signal detection matrix then allows the calculation of the discriminability measure, log d.
Compared to the original version of the White and Wixted (1999) model, however, we add an important assumption, first proposed by Brown and White (2009). This assumption recognizes that the rewards for correct matching act in a context of total reinforcement. Specifically, we assumed that the effect of the R1i/R2i reward ratio in determining the choice at stimulus value i is diluted by rewards for other behavior, Ro. If Ro acts as a general background, then it is added to R1 or R2. Accordingly, we assume that at a given stimulus value i, B1i/B2i = (R1i + Ro)/(R2i + Ro). One specific advantage of this new assumption is that it allows the prediction of the effects of absolute rate of reward on matching accuracy—with overall lower reward probabilities, discriminability is reduced (Brown & White, 2009). The original White and Wixted model did not predict this effect of absolute rate of reward, but the modified version does. Application of the model below to the results of a variety of experimental conditions assumes that the main causal factor in forgetting is the value of Ro, rewards for other behavior. The relativity of R to Ro, however, means that in any instance, forgetting could result from an increase in Ro, or a weakening of R. This possibility is illustrated by rewriting our equation: B1i/B2i = (R1i + Ro)/(R2i + Ro), after dividing top and bottom expressions by Ro, to give: B1i/B2i = (R1i / Ro + 1)/(R2i / Ro + 1). Our interpretation of the term R/Ro is that the effect of R is weakened or diluted by the effect of rewards for other behavior. An alternative interpretation, not considered here, might be that rewards for remembering are weakened by some other factor such as changing expectancies across time. In other words, the relativity of R to Ro means that variation in task parameters could result in a decrease in R that is modeled by an increase in Ro. This conclusion is plausible because a change in parameters of the memory task could be associated with a change in Ro. For example, if the sample duration is extremely short, it is plausible that Ro is higher than when the sample is of long duration and more attention or effort is being paid to the memory task.
In behavioral terms, the notion of reinforcement competition, following Herrnstein (1970), is used to account for the allocation of behavior between two or more alternatives. In our model, these alternatives are the task of remembering and alternative or other behaviors. The task of remembering may or may not include rehearsal as just one aspect. In this behavioral view, remembering is a conditional discrimination like any other but with sample stimuli (in delayed matching) temporally separated from the comparison stimuli (White, 2002a). Thus, the pigeon’s allocation of behavior to the memory task versus alternative activities is determined by the rewards for remembering relative to rewards for other behaviors. Our shorthand way of describing this differential allocation of behavior is that the pigeon may switch attention between remembering and alternative activities.
The Effect of Retention Interval
The feature that defines delayed matching as a memory task is the retention interval between presentation of the to-be-remembered sample stimuli and the comparison stimuli to which a choice response is made. For any model of remembering, the critical objective is to predict the effect of the retention interval by describing the effects of variables correlated with time. White and Wixted (1999) assumed a diffusion process in which the standard deviation of the discriminal distributions (which could be different for the two distributions—White & Wixted, 2010) increased with increasing time in the retention interval, thus increasing the overlap between distributions and decreasing discriminability. White and Wixted did not specify the form of the diffusion process.
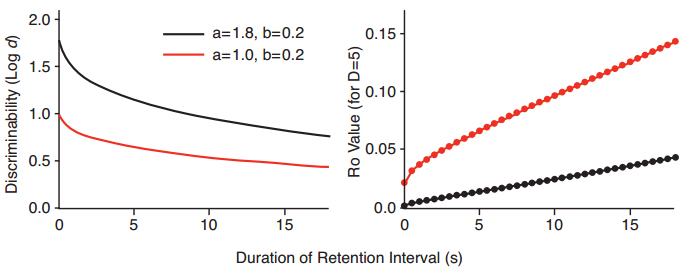
Figure 3. Hypothetical examples of exponential forgetting functions in the square root of time that differ in intercept a, but not slope b (left panel), and discrete values of Ro from the modified White-Wixted model at different times in the retention interval, needed to generate the values of discriminability for the hypothetical forgetting functions in the left panel (right panel).
However, White (2002b) showed that the specific form of diffusion could predict the mathematical form of the forgetting function. If the function relating standard deviation to time was linear, the predicted forgetting function was hyperbolic. If the function was exponential, the predicted forgetting function was exponential. If diffusion was a function of the square root of time, assuming that stimulus value drifts over time according to a random walk, the predicted forgetting function was a power function (White, 2002b). To date, however, it is not clear which form the hypothetical diffusion process might follow.
The present model does not assume a diffusion process, but predicts the effect of retention-interval duration by assuming that Ro grows with time over the course of the retention interval. This important assumption means that relative to Ro, the effectiveness of rewards for remembering decreases over time. Ro grows over time because opportunities to engage in competing activities increase with time in the retention interval. For example, in the first second into the retention interval, orienting toward the food hopper might be the only alternative. However, by 10 s, a variety of behaviors is possible. Additionally, at the beginning of the retention interval, Ro might be low because alternative behaviors had been exhausted in a previously illuminated experimental chamber during the intertrial interval (Santi, 1984), or Ro might grow at a rapid rate during the retention interval because the chamber was illuminated and allowed more possible alternative activities than in a dark retention interval.
We arrived at the Ro growth function in the following way. First, we drew two theoretical forgetting functions for y = a·exp(b·?t), with the same slope b, but with different intercepts a (Figure 3, left panel). Second, using our Excel-based implementation of the modified White-Wixted model, we asked what (punctate) values of Ro were needed in order to generate the log d values for the exponential in ?t forgetting function. These are shown in the right panel of Figure 3. We did the same thing for forgetting functions that had the same intercepts but differed in slope (Figure 4, left panel). The set of Ro values at different times in the retention interval, shown in the right panel of Figure 4, are the values needed in order to generate the exponential in ?t functions with different slopes in the left panel of Figure 4.
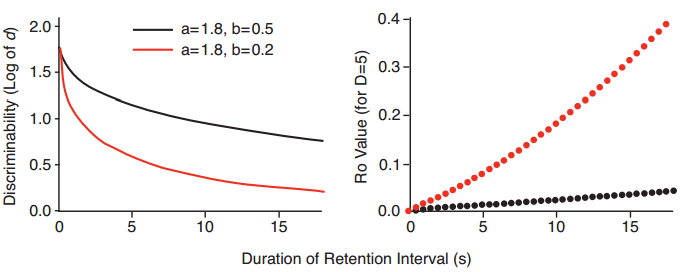
Figure 4. Hypothetical examples of exponential forgetting functions in the square root of time that differ in slope b, but not intercept a (left panel), and discrete values of Ro from the modified White-Wixted model at different times in the retention interval, needed to generate the values of discriminability for the hypothetical forgetting functions in the left panel (right panel).
The result of the back-to-front hypothetical analysis shown in Figures 3 and 4 suggested to us that an approximately linear Ro growth function was needed to achieve a reduction in discriminability with increasing retention-interval duration according to y = a·exp(b·?t). Intuitively, the growth of Ro over the course of the retention interval might be limited, and follow a Gompertz function, in which slower growth at the start is followed by a period of rapid growth, and then a falloff in growth as the function reaches a limit. Such a process might occur over a much longer time, but for the short durations used in the delayed matching task, the growth of Ro over most of the range is best approximated by a linear function. The linear function is of course the most parsimonious, and in a very different model with ‘null’ memory traces that block recall (Lansdale & Baguley, 2008), the null traces are assumed to increase as a linear function of time. We therefore assume a linear growth function that has an intercept at (0) of Ro (0), and a slope of g. That is, the growth over time t is Ro = Ro (0) + g·t.
The Ro Model
The resulting modified White-Wixted model, which we call the “Ro model” for short, has three parameters, the distance D between means of the discriminal distributions, and the intercept Ro (0) and slope g of the Ro growth function, with standard deviations of the discriminal distributions set at 1.0. When generating predicted forgetting functions from the Ro model, the intercept of the forgetting function depends on both D and the intercept of the Ro growth function, but it does not depend on the slope g of the Ro growth function. These relationships are illustrated in Figure 5, for multiple runs of the model. Figure 5 shows values of the forgetting function intercepts a, for instances in which the intercepts of the growth function vary with D = 5 (top panel), and for instances in which D varies, for a constant growth function intercept (bottom panel).
A similar hypothetical analysis shows that the slope of the predicted forgetting function depends on both the slope of the Ro growth function and its intercept. Figure 6 shows that the slope, or rate of forgetting <b, of the predicted forgetting function is greater, the greater the rate of increase in Ro over the course of the retention interval. However, if Ro starts at a higher level early in the interval (that is, at a higher intercept), the rate of growth in Ro is constrained and accordingly the rate of forgetting is not so great.
Forgetting Functions Differing in Intercept
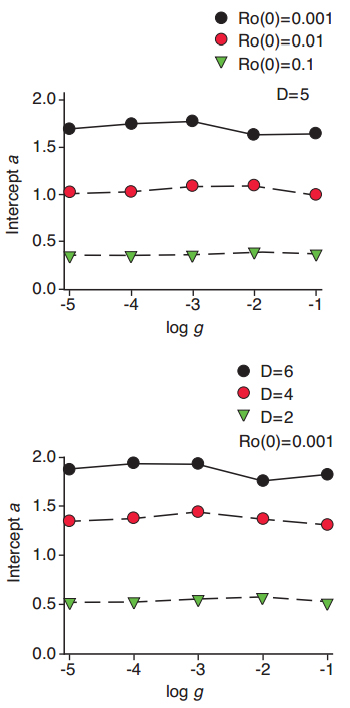
Figure 5. The intercept of predicted forgetting functions depends on the intercept of the hypothetical Ro growth function and the distance D between means of discriminal dispersions in the Ro model, but does not depend on the slope g of the growth function.
As a generalization, forgetting functions are characterized by differences in intercept, that is, discriminability at time t = 0, and in slope, or rate of forgetting (White, 1985, 2001, 2013). The following sections give examples of both. In the figures that follow, both panels show data from empirical studies of delayed matching to sample, typically in the pigeon, and in which retention interval was varied over several values. The left panel shows dashed curves for the exponential in ?t fitted to the data by the method of least squares. The right panel shows the smooth curves predicted by our Ro model. These, too, were best-fitting functions according to the method of least squares. The right panels give values for the three parameters in the model to facilitate comparison across experimental conditions.
Functions that differ in intercept can be interpreted in terms of factors that affect overall difficulty of the task, or attentional factors, such as the disparity between sample stimuli, the number of responses made to a sample, and the duration of sample stimulus presentation. In a first example, Fetterman (1995) trained pigeons to discriminate three short sample durations from three long durations in a delayed matching task, and categorized the discriminations as easy, medium, or hard. His data, plotted in terms of the nonparametric discriminability measure A’, are shown in Figure 7. The left panel shows fits of the exponential in ?t, and the right panel shows fits of the Ro model. In the Ro model, the intercept of the Ro growth function was set at 0.0001, and D and g were free to vary. As the discrimination became more difficult, D decreased and the rate of Ro growth in the retention interval increased. This effect illustrates our main interpretation of Ro, which functions to attract attention away from the task of remembering by rewarding competing behaviors, analogous to concurrent tasks in human memory research.

Figure 7. Data from Fetterman (1995) with fitted exponential in ?t functions differing primarily in intercept but not slope (left panel), and fitted functions predicted by the Ro model (right panel).
In a second example, Grant (1976) found that increasing the exposure duration of sample stimuli resulted in an increase in accuracy of pigeons’ delayed matching performance. We transformed the proportion correct (p) data from Grant’s study to Logit p, which equals log d when there is no response bias (a safe assumption for averaged data). Figure 8 shows the exponential in ?t function fitted to the data in the left panel and the functions predicted by our Ro model in the right panel. The decrease in the D parameter in the Ro model with decreasing sample duration reflects the overall weakening of the discrimination, and the increase in the rate of growth of Ro for the more difficult discrimination is similar to the effect shown in Figure 7.
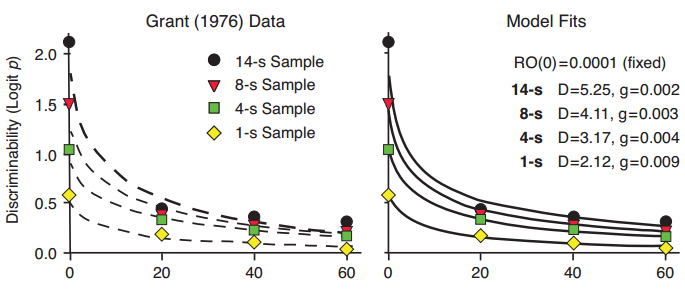
Figure 8. Data from Grant (1976) with fitted exponential in ?t functions differing primarily in intercept but not slope (left panel), and fitted functions predicted by the Ro model (right panel).
In a third example, five pecks to the sample (FR5) led to greater delayed matching accuracy than did a single peck (White & Wixted, 1999), with fitted exponential in ?t functions that differed in intercept but not slope (Figure 9, left panel). The Ro model predicts a decrease in D for FR1 compared to FR5, with an increase in the rate of Ro growth, given a fixed intercept for the Ro growth function (Figure 9, right panel).
A further manipulation to enhance the discriminability of the samples is torequire differential responding to the two samples, as did Zentall and Sherburne (1994). They trained their pigeons to respond (FR10) or not to respond (DRO) to color samples in a delayed matching task. With differential responding, discriminability was overall higher than without, and fitted exponential in ?t functions showed clear differences in intercept (Figure 10, left panel). Predictions from the Ro model (Figure 10, right panel) also fitted the data well. The difference in discrimination between the two conditions was reflected in a higher value of the D parameter for the FR10 vs. DRO task, and a lower rate of growth of Ro during the retention interval. In other words, differential responding to the sample helped to protect attention to the memory task from the interfering effects of reinforcers for alternative activities.
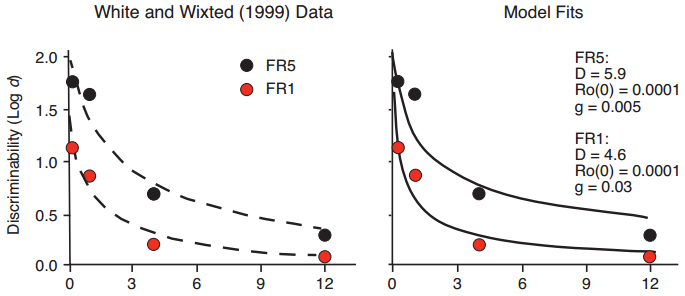
Figure 9. Data from White & Wixted (1999) with fitted exponential in ?t functions differing primarily in intercept but not slope (left panel), and fitted functions predicted by the Ro model (right panel).
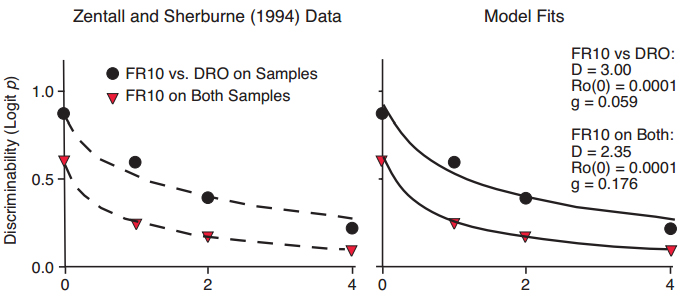
Figure 10. Data from Zentall & Sherburne (1994), with fitted exponential in ?t functions differing primarily in intercept (left panel), and fitted functions predicted by the Ro model (right panel).
The four examples above are all instances in which variation in sample-stimulus discriminability, through physical stimulus disparity, exposure duration, repetition, or differential sample responding, can be predicted by changes in the distance D between discriminal distributions in the Ro model, accompanied by an increase in the rate of Ro growth when the discrimination becomes more difficult and the distracting force of Ro becomes greater. For fits of the Ro model to data in Figures 7–10, the intercept of the Ro growth function was 0.0001 for all of the different conditions. Figure 5 suggests, however, that stimulus disparity D could be held constant for the comparison between different conditions, and variation in the intercept a of the forgetting function could be accounted for by variation in the intercept of the growth function. The Ro model would then have two free parameters, namely the intercept and slope of the growth function, and we would interpret discriminability differences at t = 0 as resulting from differences in attention to the sample at the time of encoding, versus attention to competing behaviors. The latter interpretation seems consistent with instances in which sample-stimulus conditions are held constant, but accuracy is lowered through drug administration and consequential distraction from competing alternatives. For example, administration of the drug scopolamine increases the overall difficulty of discrimination, as reflected in a reduction in the intercept of the forgetting function, consistent with much prior research on the effects of drugs on delayed matching performance in pigeons and rats (Parkes & White, 2000; White & Ruske, 2002; Wright & White, 2003). Ruske, Fisher, and White (1997) compared the effects of scopolamine with a vehicle control on delayed matching performance in pigeons. Their data are shown in Figure 11, with fitted exponential in ?t functions that differ in intercept. For fits of the Ro model (Figure 11, right panel), we assumed that sample discriminability was the same for vehicle and drug conditions, and set D = 5. In terms of the model, both the starting level of Ro (the intercept), and the rate of growth in Ro across the retention interval, were greater under scopolamine administration. The presence of higher levels of Ro under drug administration, which distracts the animal from attending to the memory task, seems plausible.
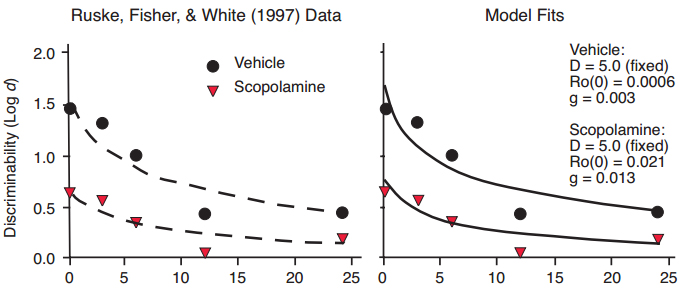
Figure 11. Data from Ruske, Fisher, & White (1997) with fitted exponential in ?t functions differing in intercept but not slope (left panel), and fitted functions predicted by the Ro model (right panel).
Forgetting Functions Differing in Slope
Rate of forgetting, or slope of the forgetting function, tends to be influenced by events occurring during the retention interval, and by reinforcement factors. The most striking example is retroactive interference, thoroughly studied by Roberts and Grant (1978), Cook (1980), and others. Pigeons, strongly visual animals, perform delayed matching tasks with visual stimuli with high accuracy when the experimental chamber is dark during the retention interval. When the chamber is illuminated during the retention interval, accuracy plummets from a high level at t = 0 s, to very low levels. During the retention interval in the illuminated chamber, they tend to peck at marks on the chamber wall, pace, wing flap, and find grain spilled from the food hopper. In other words, they engage in a variety of behaviors that we assume are extraneous to the task of remembering, and that are rewarded by (hypothetical) Ro, reinforcers for other behavior. Roberts and Grant (1978) varied the retention interval over a wide range and reported a very clear detrimental effect of illuminating the chamber by turning on the houselight. A similar result, also for pigeons in a delayed matching task, was reported by Harper and White (1997). Their data (Figure 12) were well fitted by exponential in ?t functions that differed in slope but not intercept (Figure 12, left panel). Their data were also satisfactorily fitted by our Ro model, with the same values for the D parameter for dark and houselight conditions, with similar values for the intercepts of the Ro growth functions, and a greater growth of Ro under conditions with the houselight turned on (Figure 12, right panel). In this and subsequent examples in which slope of the forgetting function varies, D was held constant across conditions, and only the two growth function parameters were free to vary. This result provides strong validation for our assumption that Ro grows during the retention interval and rewards extraneous behaviors that compete with the task of remembering.

Figure 12. Data from Harper & White (1997), with fitted exponential in ?t functions differing primarily in slope but not intercept (left panel), and fitted functions predicted by the Ro model (right panel).
The assumption that the level of Ro during the retention interval may depend on whether the chamber is dark or light gains support from a novel result reported recently by White and Brown (2011). Retention interval duration was varied within sessions in a delayed matching task with pigeons. Three conditions are of interest, two of which replicated the effect shown in Figure 12. In the third, the chamber was illuminated for the first few seconds of the retention interval and accuracy at these retention intervals was low. When the chamber was darkened after the first few seconds in longer retention intervals, accuracy recovered to the higher level consistent with performance in the baseline condition in which the retention intervals were dark throughout. In terms of our Ro model, we assume that Ro was high during the initially light part of the retention interval and lower during the later dark part of the interval, thus causing an apparent reversal of the forgetting function.
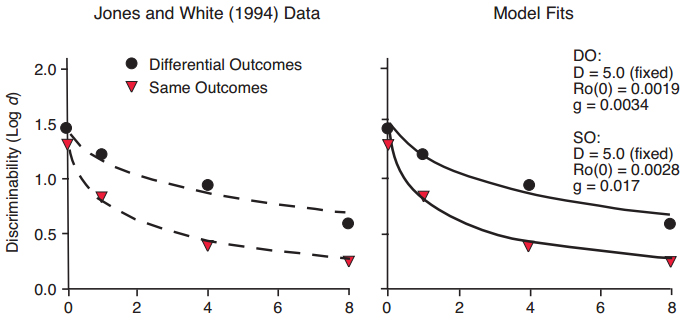
Figure 13. Data from Jones & White (1994), with fitted exponential in ?t functions differing primarily in slope but not intercept (left panel), and fitted functions predicted by the Ro model (right panel).
The differential outcomes effect (DOE) is a curious phenomenon in which discriminability is enhanced when the outcomes or rewards for correct matching responses are different, compared to when they are the same (Urcuioli, 2005). Our previous analyses indicate that the DOE manifests primarily as a difference in rate of forgetting, that is, in the slope of the forgetting function, often with relatively small differences in intercepts (Jones & White, 1994). In other words, the enhanced discriminability appears at longer delay intervals to a greater extent than at shorter delays. The DOE is illustrated in Figure 13 (left panel), in which the data from the within-sessions procedure reported by Jones and White are fitted by exponential in ?t functions that differ mainly in slope. The data are also well fitted by our Ro model (Figure 13, right panel), with an assumption that stimulus disparity D is equal for same and differential outcomes trials. The DOE in Figure 13 is predicted by starting with a larger background Ro on Same trials than on Different trials, and grows at a faster rate (g) on Same trials. This assumption makes sense if it is assumed that rewards on Different trials have a stronger effect than on Same trials and are less diluted by Ro (as in the signaled probability effect described below), consistent with the finding that rewards in mixed or variable schedules of reinforcement have stronger effects in maintaining behavior than do rewards in fixed schedules of reinforcement (Davison, 1969; Fantino, 1967).

Figure 14. Data from Miller, Freidrich, Narkavik, & Zentall (2009), with fitted exponential in ?t functions differing primarily in slope (left panel), and fitted functions predicted by the Ro model (right panel).
A possible challenge to our notion that the DOE derives from a greater reinforcing effect of the differential outcomes, relative to Ro during the retention interval, comes from the unusual finding that the DOE occurs with non-hedonic differential outcomes. Figure 14 shows the delayed matching-to-sample performance of pigeons for which outcomes for correct choices in a differential outcomes condition were brief presentations of houselight or tone, followed by the same amount of food, compared to either houselight or tone plus food in a non-differential outcomes condition (Miller, Friedrich, Narkavic, & Zentall, 2009). The data follow the same form as those in Figure 13 in which differential hedonic (food) outcomes were arranged, and were well fit by exponential in ?t functions differing primarily in slope (left panel) and by our Ro model (right panel). In terms of our Ro model, we suggest that the same account applies to the DOE with differentially cued food outcomes (Figure 14) as for differential food outcomes (Figure 13). Specifically, by preceding rewards for correct choices following the different sample stimuli by different brief signals, the reinforcing strength of the rewards is enhanced relative to the effect of Ro. As a result, the interfering effect of Ro on different-outcome trials is less than that on same-outcome trials. The effect of adding the cue is perhaps consistent with the higher response rates in the choice phase of a concurrent-chains procedure when the choice leads to multiple schedules that are differentially cued, compared to when the choice leads to mixed schedules that are not (Hursh & Fantino, 1974).
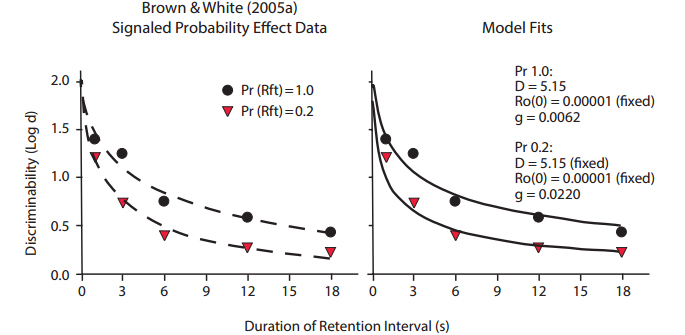
Figure 15. Data from Brown & White (2005a), with fitted exponential in ?t functions differing primarily in slope but not intercept (left panel), and fitted functions predicted by the Ro model (right panel).
The signaled probability effect occurs in delayed matching to sample when a cue is presented during the retention interval (but not with the sample), which signals whether correct matching responses will be rewarded with low or high probability. The reinforcer probabilities and associated cues alternate randomly across trials within session, and in the study reported by Brown and White (2005a), were 0.2 and 1.0. Figure 15 shows their data, with best-fitting exponential in ?t functions that differed in slope but not intercept (left panel). The right panel of Figure 15 shows the fits of our Ro model, in which parameters for stimulus disparity D and the intercept of the Ro growth function (at t = 0) were the same for the two probability conditions, as is intuitively plausible. The difference in the model fits was in the rate of Rogrowth parameter, g. This result validates our interpretation. If the reduction in discriminability with increasing retention interval duration results from competition between reinforcers for completing the memory task and reinforcers for alternative or other behaviors, Ro, then a reduction in the probability of reward for the memory task will result in a relatively greater influence of Ro and, accordingly, a greater increase in the rate of forgetting.
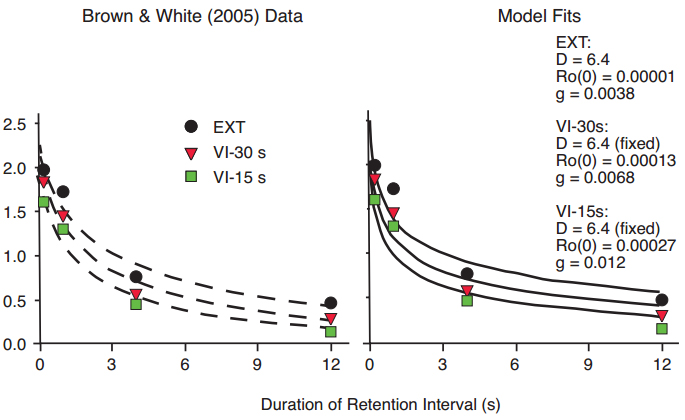
Figure 16. Data from Brown & White (2005b), with fitted exponential in ?t functions differing primarily in slope but not intercept (left panel), and fitted functions predicted by the Ro model (right panel), for conditions in which center-key pecking during the retention interval (an extraneous task) was reinforced according to VI 15 s, VI 30 s, or EXT schedules.
The rationale above was applied more specifically by Brown and White (2005b) to a delayed matching-to-sample task with pigeons, in which an extraneous task was interpolated in the retention interval. The extraneous task involved pecking the center key, with pecks rewarded according to variable interval (VI) schedules of VI 15 or VI 30 s, or not at all (Extinction or EXT). The rationale was that the experimenter-arranged extraneous VI reinforcement should add to the hypothetical Ro to increase the total extraneous reinforcement. The data were satisfactorily fit by exponential in ?t functions (Figure 16, left panel), and by our Ro model (right panel). In terms of the model, for a fixed value of the stimulus disparity parameter D, both the intercept and slope of the Ro growth function increased with increasing rate of extraneous reinforcement. The reduction in accuracy in delayed matching performance with increasing rate of extraneous reinforcement for center-key responding can therefore be attributed to interference or competition between reinforcers for other behavior and reinforcers for completing the delayed matching task. That is, the result reported by Brown and White (2005) constitutes strong direct support for our Ro theory.
In the delayed matching task, the reinforcement context might extend to the intertrial interval (ITI), as well as the retention interval, perhaps depending on the extent to which the ITI is discriminated from the trial. During the ITI, extraneous behaviors may occur. Following the argument of McLean and White (1983) and McLean (1991), Ro not obtained in a short ITI might carry over into a subsequent trial and compete with rewards for the delayed matching task. As a result, accuracy with short ITIs is poorer than with long ITIs, a common result (Edhouse & White, 1988; Roberts, 1980; White, 1985). Additionally, adding noncontingent reinforcers to the ITI (Santi & Roberts, 1985), especially when they are added at the end of the ITI (Spetch, 1985), results in a substantial reduction in matching accuracy. When the ITI is illuminated and the retention interval is dark, however, the trial spacing effect is lost (Edhouse & White, 1988; Santi, 1984), presumably because a clearer discrimination between the ITI and retention interval reduces the likelihood of carryover of Ro.
Conclusion
In the present paper, we suggest that forgetting in delayed matching-to-sample tasks results from competition between reinforcers for extraneous behaviors and the reinforcers for matching to sample. As a result, extraneous behaviors interfere or compete with matching to sample. The notion of reinforcer competition is well developed in the study of concurrent choice and applications of the matching law (Davison & McCarthy, 1988). Even at the time of sample presentation, attention to the memory task may be diminished by distraction caused by reinforcers for other behaviors.
In our modification of the White-Wixted (1999) model, the parameter D represents the distance between means of the discriminal dispersions, as in the original version of the model. In the first several examples we present, D was free to vary in fitting the model, and tended to change in plausible ways with apparently decreasing difficulty of the discrimination. For example, Grant (1976) found decreasing accuracy with shorter presentation durations of the sample stimuli (Figure 8). In our fits of the model to Grant’s data, D decreased systematically with decreasing sample presentation duration. The intercepts of both obtained and predicted forgetting functions also decreased. As Figure 5 shows, however, the intercept can be determined by an additive combination of D and the intercept Ro (0) of the Ro growth function. That is, given a particular level of stimulus disparity, the background Ro at the beginning of the retention interval, or during sample presentation, can result in lack of attention to the sample and a decrease in discriminability. It is therefore possible to substitute changes in Ro (0) for changes in D, thus requiring only two free parameters in the Ro model, both relating to reinforcers for extraneous behavior. Consistent with this possibility, in some of the examples above, such as the effect of scopolamine in reducing overall accuracy (Figure 11), an increase in the intercept of the Ro growth function contributed to the reduction in the intercept of the forgetting function.
The main feature of the present Ro model is the assumption that Ro grows over the course of the retention interval, and that this growth is the cause of forgetting, that is, the progressive reduction in discriminability with the passage of time. This assumption and its implementation in our modification of the White-Wixted model allowed quantitative predictions of the time course of forgetting functions. Our assumption of the linear growth function is justified by the success of our Ro model in fitting the data. Although we have not reported measures of goodness of fit, the figures above show that the fits of the Ro model mirrored the fits of the exponential in ?t function, which is the most successful function in fitting data from delayed matching studies (White, 2001, 2002b). When we considered alternative Ro growth functions, such as a limited growth exponential and the Gompertz function, they were essentially linear over the range of delays used in most of the studies reviewed, and so had no advantage over the linear function adopted here. The linear function might seem counterintuitive, but we see no reason why reinforcers from distracting sources should not continue to build up linearly as time progresses. The Ro model is somewhat parsimonious. It can be regarded as an interference model with a single primary mechanism—reinforcement competition. It has only three parameters, stimulus disparity D, the starting level of Ro, and the rate of growth of Ro over the course of the retention interval, or only two parameters when D is fixed. Quantitatively, it does well to fit delayed matching data from studies with a range of independent variables. We have not yet compared it with other possible models, in particular the reinforcement-based model of Nevin, Davison, Odum, and Shahan (2007), or conducted a comprehensive survey of its ability to fit data from all extant delayed matching studies with at least four delays. Its ultimate success, however, may depend on more intuitive considerations. For example, when fits of the model with two or three free parameters indicate that hypothetical Ro is responsible for an effect, such as in the differential outcomes effect (see Figures 13 and 14), it will be necessary to provide validating evidence to reveal the action of extraneous rewards in diluting the effects of rewards for remembering.
References
Baddeley, A. (1997). Human memory: Theory and practice. Revised edition. Hove, UK: Psychology Press.
Blough, D. S. (1959). Delayed matching in the pigeon. Journal of the Experimental Analysis of Behavior, 2, 151-160. doi.org/10.1901/jeab.1959.2-151
Brown, G. S., & White, K. G. (2005a). On the effects of signalling reinforcer probability and magnitude. Journal of the Experimental Analysis of Behavior, 83, 119-128. doi.org/10.1901/jeab.2005.94-03
Brown, G. S., & White, K. G. (2005b). Remembering: The role of extraneous reinforcement. Learning & Behavior, 33, 309-323. doi.org/10.3758/BF03192860
Brown, G. S., & White, K. G. (2009). Reinforcer probability, reinforcer magnitude, and the
reinforcement context for remembering. Journal of Experimental Psychology: Animal Behavior Processes, 35, 238-249. doi.org/10.1037/a0013864
Brown, J. (1958). Some tests of the decay theory of immediate memory. Quarterly Journal of Experimental Psychology, 10, 12-21. doi. org/10.1080/17470215808416249
Cook, R. G. (1980). Retroactive interference in pigeon short-term memory by a reduction in ambient illumination. Journal of Experimental Psychology: Animal Behavior Processes, 6, 326-338. doi. org/10.1037/0097-7403.6.4.326
Davison, M. C. (1969). Preference for mixed-interval versus fixed-interval schedules. Journal of the Experimental Analysis of Behavior, 12, 247-252. doi. org/10.1901/jeab.1972.17-169
Davison, M., & McCarthy, D. (1988). The Matching Law: A research review. Hillsdale, NJ: Erlbaum.
Davison, M. C., & Tustin, R. D. (1978). The relation between the generalized matching law and signal detection theory. Journal of the Experimental Analysis of Behavior, 29, 331-336. doi.org/10.1901/jeab.1978.29-331
Edhouse, W., & White, K.G. (1988). Sources of proactive interference in animal memory. Journal of Experimental Psychology: Animal Behavior Processes, 14, 56-71. doi.org/10.1037/0097-7403.14.1.56
Fantino, E. (1967). Preference for mixed- versus fixed-ratio schedules. Journal of the Experimental Analysis of Behavior, 10, 35-43. doi.org/10.1901/ jeab.1967.10-35
Fetterman, J. G. (1995). The psychophysics of remembered duration. Animal Learning & Behavior, 23, 49-62. doi.org/10.3758/BF03198015
Grant, D. S. (1976). Effect of sample presentation time on long-delay matching in the pigeon. Learning and Motivation, 7, 580-590. doi. org/10.1016/0023-9690(76)90008-4
Grant, D. S. (1981). Short-term memory in the pigeon. In N. E. Spear & R. R. Miller (Eds.), Information processing in animals: Memory mechanisms (pp. 227-256). Hillsdale, NJ: Erlbaum.
Harper, D. N., & White, K.G. (1997). Retroactive interference and rate of forgetting in delayed matching-to-sample performance. Animal Learning & Behavior, 25, 158-164. doi.org/10.3758/BF03199053
Herrnstein, R. J. (1961). Relative and absolute strength of response as a function of frequency of reinforcement. Journal of the Experimental Analysis of Behavior, 4, 267-272. doi.org/10.1901/jeab.1961.4-267
Herrnstein, R. J. (1970). On the law of effect. Journal of the Experimental Analysis of Behavior, 13, 243-266. doi.org/10.1901/jeab.1970.13-243
Hursh, S. R., & Fantino, E. (1974). An appraisal of preference for multiple versus mixed schedules. Journal of the Experimental Analysis of Behavior, 22, 31-38. doi.org/10.1901/jeab.1974.22-31
Jones, B. M., & White, K. G. (1994). An investigation of the differential-outcomes effect within sessions. Journal of the Experimental Analysis of Behavior, 61, 389-406. doi.org/10.1901/jeab.1994.61-389
Lansdale, M., & Baguley, T. (2008). Dilution as a model of long-term forgetting.
Psychological Review, 115, 864-892. doi.org/10.1037/a0013325
Lewandowsky, S., Oberauer, K., & Brown, G. D. A. (2009). No temporal decay in verbal short-term memory. Trends in Cognitive Sciences, 13, 120-126. doi.org/10.1016/j.tics.2008.12.003
McGeoch, J. A. (1932). Forgetting and the law of disuse. Psychological Review, 39, 352-370. doi.org/10.1037/h0069819
McLean, A. P. (1991). Local contrast in behavior allocation during multiple-schedule components. Journal of the Experimental Analysis of Behavior, 56, 81-96. doi.org/10.1901%2Fjeab.1991.56-81
McLean, A. P., & White, K.G. (1983). Temporal constraint on choice: Sensitivity and bias in multiple schedules. Journal of the Experimental Analysis of Behavior, 39, 405-426. doi.org/10.1901/jeab.1983.39-405
Miller, H. C., Friedrich, A. M., Narkavic, R. J., & Zentall, T. R. (2009). A differential-outcomes effect using hedonically nondifferential outcomes with delayed matching to sample by pigeons. Learning & Behavior, 37, 161-166. doi.org/10.3758/LB.37.2.161
Nairne, J. S. (2002). Remembering over the short-term: The case against the standard model. Annual Review of Psychology, 53, 53-81. doi.org/10.1146/annurev.psych.53.100901.135131
Nevin, J. A., Davison, M., Odum, A. L., & Shahan, T.A. (2007). A theory of attending, remembering, and reinforcement in delayed matching to sample. Journal of the Experimental Analysis of Behavior, 88, 285-317. doi.org/10.1901/jeab.2007.88-285
Parkes, M., & White, K. G. (2000). Glucose attenuation of memory impairments. Behavioral Neuroscience, 114, 1-13. doi.org/10.1037//0735-7044.114.2.307
Peterson, L. R., & Peterson, M. (1959). Short-term retention of individual verbal items. Journal of Experimental Psychology, 58, 193-198. doi.org/10.1037/h0049234
Portrat, S., Barrouillet, P., & Camos, V. (2008). Time-related decay or interference-based forgetting in working memory? Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 1561-1564. doi.org/10.1037/a0013356
Roberts, W. A. (1972). Short-term memory in the pigeon: Effects of repetition and spacing. Journal of Experimental Psychology, 94, 74-83. doi.org/10.1037/h0032796
Roberts, W. A. (1980). Distribution of trials and intertrial retention in delayed matching to sample with pigeons. Journal of Experimental Psychology: Animal Behavior Processes, 64, 217-237. doi.org/10.1037/0097-7403.6.3.217
Roberts, W. A., & Grant, D. S. (1978). An analysis of light-induced retroactive inhibition in pigeon short-term memory. Journal of Experimental Psychology: Animal Behavior Processes, 4, 219-236. doi.org/10.1037/0097-7403.4.3.219
Roediger, H. L. III., Weinstein, Y., & Agarwal, P. K. (2010). Forgetting: Preliminary considerations. In S. D. Salla (Ed.), Forgetting (pp. 1-22). Hove, Sussex: Psychology Press.
Rubin, D. C., & Wenzel, A. E. (1996). One hundred years of forgetting: A quantitative description of retention. Psychological Review, 103, 734-760. doi.org/10.1037/0033-295x.103.4.734
Ruske, A. C., Fisher, A., & White, K. G. (1997). Attenuation of scopolamine-induced deficits in delayed-matching performance by a new muscarinic agonist. Psychobiology, 25, 313-320.
Santi, A. (1984). The trial spacing effect in delayed matching-to-sample by pigeons is dependent upon the illumination condition during the intertrial interval. Canadian Journal of Psychology, 38, 154-165. doi.org/10.1037/h0080830
Santi, A., & Roberts, W. A. (1985). Reinforcement expectancy and trial spacing effects in delayed matching-to-sample by pigeons. Animal Learning & Behavior, 13, 274-284. doi.org/10.3758/BF03200021
Sargisson, R. J., & White, K. G. (2003). On the form of the forgetting function: The effects of arithmetic and logarithmic distributions of delays. Journal of the Experimental Analysis of Behavior, 80, 295-309. doi.org/10.1901/jeab.2003.80-295
Spetch, M. L. (1985). The effect of intertrial interval food presentations on pigeons’ delayed matching to sample accuracy. Behavioural Processes, 11, 309-315. doi.org/10.1016/0376-6357(85)90025-7
Staddon, J. E. R. (1983). Adaptive behavior and learning. Cambridge: Cambridge University Press.
Suprenant, A. M., & Neath, I. (2009). Principles of memory. NewYork: Psychology Press.
Thurstone, L. L. (1927). A law of comparative judgment. Psychological Review, 34, 273-286. doi.org/10.1037/h0070288
Urcuioli, P. J. (2005). Behavioral and associative effects of differential outcomes on discrimination learning. Learning & Behavior, 33, 1-21. doi.org/10.3758/BF03196047
White, K. G. (1985). Characteristics of forgetting functions in delayed matching to sample. Journal of the Experimental Analysis of Behavior, 44, 15-34. doi.org/10.1901/jeab.1985.44-15
White, K. G. (2001). Forgetting functions. Animal Learning & Behavior, 29, 193-207. doi.org/10.3758/BF03192887
White, K. G. (2002a). Psychophysics of remembering: The discrimination hypothesis. Current Directions in Psychological Science, 11, 141-145. doi.org/10.1111/1467-8721.00187
White, K. G. (2002b). Temporal generalization and diffusion in forgetting. Behavioral Processes, 57, 121-129. doi.org/10.1016/S0376-6357(02)00009-8
White, K.G. (2012). Dissociation of short term forgetting from the passage of time. Journal of Experimental Psychology: Learning, Memory, and Cognition, 38, 255-259. doi.org/10.1037/a0025197
White, K. G. (2013). Remembering and forgetting. In Madden, G. J. (Ed.-in-Chief), W. V. Dube, T. Hackenberg, G. P. Hanley, & K. A. Lattal (Assoc. Eds.) APA handbooks in psychology: APA Handbook of behavior analysis, Volume. 1: Methods and principles. Washington, DC: American Psychological Association.
White, K.G., & Brown, G. S. (2011). Reversing the course of forgetting. Journal of
the Experimental Analysis of Behavior, 96, 177-189. doi.org/10.1901/jeab.2011.96-177
White, K. G., & Ruske, A. C. (2002). Memory deficits in Alzheimer’s Disease: The encoding hypothesis and cholinergic function. Psychonomic Bulletin & Review, 9, 426-437. doi.org/10.3758/BF03196301
White, K.
G., & Wixted, J. T. (1999). Psychophysics of remembering. Journal of the Experimental Analysis of Behavior, 71, 91-113. doi.org/10.1901/jeab.1999.71-91
White, K. G., & Wixted, J. T. (2010). Psychophysics of remembering: To bias or not to bias? Journal of the Experimental Analysis of Behavior, 94, 83-94. doi.org/10.1901/jeab.2010.94-83
Wixted, J. T. (2004). The psychology and neuroscience of forgetting. Annual Review of Psychology, 55, 235-269. doi.org/10.1901/jeab.2010.94-83
Wixted, J. T. (2010). The role of retroactive interference and consolidation in everyday forgetting. In S. D. Salla (Ed.), Forgetting (pp. 285-312). Hove, Sussex: Psychology Press.
Wixted, J. T., & Carpenter, S. K. (2007). The Wickelgren Power Law and the Ebbinghaus Savings Function. Psychological Science, 18, 133-134. doi.org/10.1111/j.1467-9280.2007.01862.x
Wixted, J. T., & Ebbesen, E. B. (1991). On the form of forgetting. Psychological Science, 6, 409-415. doi. org/10.1111/j.1467-9280.1991.tb00175.x
Wright, F. K., & White, K. G. (2003). Effects of methylphenidate on working memory in pigeons. Cognitive, Affective & Behavioral Neuroscience, 3, 300-308. doi.org/10.3758/CABN.3.4.300
Woodworth, R. S., & Schlosberg, H. (1954). Experimental psychology: Revised edition. New York: Holt, Rinehart and Winston.
Zentall, T. R. (1973). Memory in the pigeon: Retroactive inhibition in a delayed matching task. Bulletin of the Psychonomic Society, 1, 126-128.
Zentall, T. R., & Sherburne, L. M. (1994).The role of differential sample responding in the differential outcomes effect involving delayed matching by pigeons. Journal of Experimental Psychology: Animal Behavior Processes, 20, 390-401. doi. org/10.1037/0097-7403.20.4.390
