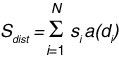MODEL DESCRIPTION

The model TraceFossil is a form of "individual based model" (IBM) in which autonomous simulated animals make decisions based on spatially explicit aspects of their environment (Grimm and Railsback 2005). These models are widely used in wildlife ecology, urban planning, and other fields, where they are frequently termed "agent models. "

TraceFossil is based on the model first used in Plotnick (2003) and is described in more detail in Koy and Plotnick (2007), which focused on patterns of movement within patches as a consequence of contact chemoreception. The latter paper discussed simulated movement patterns that were the consequence of different spatial distributions of resources within patches and resembled many random, spiral, and meandering traces. The current paper examines movements among patches, rather than movement within patches. The primary focus is on the importance of distance chemoreception to locating spatially isolated resource sites.

Space in TraceFossil is represented as a two-dimensional (2-D) or three-dimensional (3-D) square lattice. The distribution of resources in the space is represented as real numbers, ranging from 0.00 to 1.00, assigned to each node in the lattice. The model provides numerous options for the spatial distribution of these resources. This paper focuses on 2-D patterns, which simulate spatial distributions at or parallel to the sediment-water interface with different degrees of patchiness. A later paper will consider movements in three dimensions.

In the simplest case, all nodes have some level of resource chosen from an even random distribution (Figure 1.1); i.e., the resources are heterogeneous but not patchy. In the remaining cases, the level of resources at each node is again selected from an even distribution but a fixed proportion of nodes are randomly set to zero. This produces a pattern of isolated resource patches of random size and shape; the greater the proportion of the nodes set to zero, the greater the patchiness of the resource distribution. A map showing a pattern where 95% of the nodes are empty is shown in Figure 1.3.

Each node releases a chemical signal proportional to the amount of resource it contains. Detection of the signal can be either through contact or distant chemoreception. The node containing the organism is at zero; that is, all its resources are assumed to have been consumed.

For contact chemoreception, the animal is in direct contact with the adjacent eight nodes (Figure 2). The chemical signal S_contact detected at a node is assumed to be linear with the amount of resource at each node.

Distant chemoreception is modeled by assuming that each of the eight adjacent nodes (Figure 3.1) receives a summed chemical signal from N neighborhood sites that are within a defined distance R and that the organism can sense the relative signal in each of those neighboring sites. In Figure 3.2, the signal in each adjacent node comes from the N = 12 sites within R = 2; arrows represent the signal from some of these cells. A total of 34 sites are within the chemosensory range of the organism (Figure 3.1). The signal from each of these more distant cells is a function of the amount of resource it contains and attenuation due to distance (width of the arrows in Figure 3.2); that is, a nearby cell with less resource can produce more detectable chemicals than a more distant cell with greater resources.

Specifically, the signal S_dist in one of the eight adjacent cells can be written as:

where s_i is the amount of resource in the ith node within the neighborhood and a(d_i) is the signal received from that node as a function of its distance. The algorithm postulates that the chemical signals become mixed as they approach the animal. The simulated organism cannot determine directly where a node with the greatest amount of resource is located; instead it can only determine in what direction the greatest and/or closest concentrations exist.

The higher the value of R, the more likely the simulated organism is to detect distant resources; it is a proxy for the detection range of the organism. However, because the number of cells N included increases proportional to R², this number rapidly becomes very large. In addition, due to attenuation the contribution from distant nodes is very small. For these reasons, the maximum value of R utilized was 7 in nearly all cases.

Several functions are available in TraceFossil to represent signal attenuation; they are designed to include a wide range of realistic representations of chemical dispersal. The functions are based on those used to model seed dispersal by Plotnick and Gardner (2002) and are fully described therein. In this paper, attenuation is assumed to be a function of the inverse square root of distance; e.g., doubling the distance decreases the signal received by 25%. Using this function, the signal distribution detected by the example organism is shown in Figure 3.3.

Simulations with a circular neighborhood represent situations with little or no directional current. Currents are easily represented, however, by setting the attenuation functions for sites in certain directions to zero. This is equivalent to restricting the neighborhood to only those sites lying in a particular direction. For example, in Figure 4, the nodes contain a signal only from the sites directly "North" of it.

For the simulations described here, contact chemoreception has precedence over distant chemoreception; i.e., if an organism is in direct contact with a resource site, it will exploit it prior to searching for more distant resources.

During each step of a simulation, the organism:

1. Examines the eight adjacent nodes and the node with the highest value of S_contact is determined.

2. If this maximum value is not zero, then the organism moves into the node with the maximum value and "ingests" the resource in that node, reducing its level to zero.

3. If the maximum value of S_contact is zero, then all of the adjacent nodes are empty. The organism examines the eight adjacent nodes and finds the one with the highest value of S_dist. It then moves into that node.

4. If the maximum value of S_dist is zero, then there are no resources within the detection range of the organism. In that case, it moves one step in a random direction (another available option is to continue to move in the same direction as it did in the previous step).

The behavior described by this model is simple: the organism detects a chemical signal and moves in the direction of its highest value. If it encounters a food source, it ingests it. In other words, the only behaviors are chemotaxis and feeding. Examples of trails corresponding to the studied resource distributions are shown in Figure 1.1-1.3.

As with all models, there is an unavoidable trade-off of generality with specificity. It is not the goal of TraceFossil to reproduce the morphology of specific ichnotaxa (although it can potentially be modified to do so), but instead to act as a heuristic tool (sensu Hammer 1998) for understanding the behavioral and environmental control of trace-producing movements. Similarly, it is also recognized that additional factors, such as the presence of predators or substrate consistency, may also influence movement patterns (Phillips 1978). These factors will be included in subsequent versions of the model.

Gain Curves

Gain curves are plots of cumulative amounts of resource harvested over time (Olsson et al. 2001). The shape of a gain curve should relate to a forager's decision when to abandon a food patch; i.e., a flattening of the gain curve may signal depletion of the patch. On a landscape scale, the shape of the gain curve gives a measure of the forager's ability to locate high quality patches. An organism with a greater ability to locate and discriminate among patches should have a steeper gain curve than an organism that accounts patches by chance or that does not distinguish poor from rich patches. This difference should become more pronounced as patchiness increases.

Gain curves, therefore, should discriminate among foraging model organisms with different ranges of sensory ability in environments of different degrees of patchiness.

Simulations

Three sets of simulations were run. Each set possessed a different amount of patchiness - Set 1: all sites randomly occupied by resource (Figure 1.1); Set 2: 20% of the sites randomly occupied by resources (Figure 1.2), for this map, the average nearest neighbor distance between occupied sites is 1.3; Set 3: 5% of the sites randomly occupied by resources (Figure 1.3), with a mean nearest neighbor distance of 2.3. The map generated for each set was saved and reused. All maps were 100 x 100 pixels, resource values per node randomly ranged from 0.00 to 1.00, so that the average resource per node was 0.5.

Four "species" of digital organism were run on each map. Species A simply wandered randomly; it had no outside knowledge of the resource distribution. Species B possessed only contact chemoreception. Species C and D possessed both contact and distant chemoreception, but the detection range of C was R = 4 and for D it was R = 7. Average gain curves for 10 multiple runs were determined for each species and map combination.

Each run was initialized in the middle of the map. Runs were terminated when the digital organism's sensory range encountered the edge or after 200 steps. For each set of runs, the mean resource gained per step was determined (Table 1).

An additional set of runs was performed on the 5% map to evaluate the role of directional currents. For these runs, the signal attenuated linearly with distance and that the detection range was longer (R= 7 and R = 10). Only nodes to the northeast, north, and northwest contributed to the signal. The goal was to at least crudely mimic turbulent mixing upstream and the reduced attenuation associated with mass fluid transport. Because of the directionality of the current, the run was initialized at the bottom of the map.