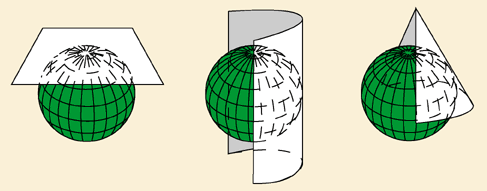
There are three types of projection surfaces:

• Azimuthal or plane
• Cylindrical
• Conic

Where do you think distortion might occur on these projections?

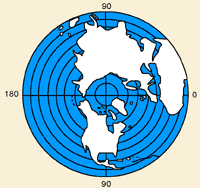
A flat projection surface is known as a "plane" or "azimuthal" projection. Imagine taking a flat piece of cardboard and placing it against a globe. Pretend that the globe is transparent, but that you can see the outline of the graticule and the continents. Inside the globe there is a light source and it makes the outlines of the graticule and land features cast a shadow on the piece of cardboard. If you could capture the shadow that was cast on the cardboard, the way the shadow lands on the cardboard would be called an "azimuthal" or "plane" projection.

Where would an "azimuthal" projection suffer the most distortion? Maps of the north and south polar regions are often "plane" or "azimuthal" projections. Why do you think this is? Polar regions are particularly well-suited to "plane" projections because the least distortion occurs near the centre of the projection image.

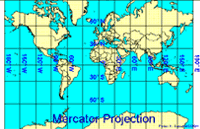
Another type of projection is a "cylindrical" projection. Again, imagine a transparent globe with a light source that casts the shadow of the outlines of its graticule and continents. Imagine rolling a piece of light cardboard into a cylinder shape around the globe and the shadows cast on to your piece of light cardboard could be captured. The resulting image, when rolled flat, would be a cylindrical projection. A Mercator projection is an example of a cylindrical projection surface. A Mercator projection does not show the north or south pole however. Why do you think this is? Where does the most distortion occur on a Mercator projection map? Look at Greenland on a Mercator projection map of the world, and then look at Australia. Compare these two countries' size and shape on a globe. The one big issue with Mercator projection maps is that shapes become very distorted the closer to the north or south pole you are and Mercator projections make it seem as though Greenland were three times the size of Australia!

The last type of projection is called a conical projection. Again, you have a piece of light cardboard, but this time you roll it up into a cone shape. Placed on the transparent globe together, cone and globe resemble an ice-cream cone. An example of a conical projection would look like this. Where would the distortion be on a conical projection? Think about where the cardboard touches the globe. Where the cardboard would touch the globe, the most accurate representation would occur. Where the cardboard is farther away, and not touching the globe, much more distortion occurs.